Telecom Churn Case Study

This analysis is the combined effort of Umaer and me.

Telecom Churn Case Study - Part 2

This notebook contains

Test Train Split
Class Imbalance
Standardization
Modelling
- Model 1 : Logistic Regression with RFE & Manual Elimination ( Interpretable Model )
- Model 2 : PCA + Logistic Regression
- Model 3 : PCA + Random Forest Classifier
- Model 4 : PCA + XGBoost

For the previous steps, refer to Part-1

1import numpy as np
2import pandas as pd
3import matplotlib.pyplot as plt 
4import seaborn as sns
5# import tabulate 
6import warnings 
7pd.set_option('display.max_columns', None)
8pd.set_option('display.max_rows', None)
9warnings.filterwarnings('ignore')

1data = pd.read_csv('cleaned_churn_data.csv', index_col='mobile_number')
2data.drop(columns=['Unnamed: 0'], inplace=True)
3data.head()

	onnet_mou_6	onnet_mou_7	onnet_mou_8	offnet_mou_6	offnet_mou_7	offnet_mou_8	roam_ic_mou_6	roam_ic_mou_7	roam_ic_mou_8	roam_og_mou_6	roam_og_mou_7	roam_og_mou_8	loc_og_t2t_mou_6	loc_og_t2t_mou_7	loc_og_t2t_mou_8	loc_og_t2m_mou_6	loc_og_t2m_mou_7	loc_og_t2m_mou_8	loc_og_t2f_mou_6	loc_og_t2f_mou_7	loc_og_t2f_mou_8	loc_og_t2c_mou_6	loc_og_t2c_mou_7	loc_og_t2c_mou_8	loc_og_mou_6	loc_og_mou_7	loc_og_mou_8	std_og_t2t_mou_6	std_og_t2t_mou_7	std_og_t2t_mou_8	std_og_t2m_mou_6	std_og_t2m_mou_7	std_og_t2m_mou_8	std_og_t2f_mou_6	std_og_t2f_mou_7	std_og_t2f_mou_8	std_og_mou_6	std_og_mou_7	std_og_mou_8	isd_og_mou_6	isd_og_mou_7	isd_og_mou_8	spl_og_mou_6	spl_og_mou_7	spl_og_mou_8	og_others_6	og_others_7	og_others_8	loc_ic_t2t_mou_6	loc_ic_t2t_mou_7	loc_ic_t2t_mou_8	loc_ic_t2m_mou_6	loc_ic_t2m_mou_7	loc_ic_t2m_mou_8	loc_ic_t2f_mou_6	loc_ic_t2f_mou_7	loc_ic_t2f_mou_8	loc_ic_mou_6	loc_ic_mou_7	loc_ic_mou_8	std_ic_t2t_mou_6	std_ic_t2t_mou_7	std_ic_t2t_mou_8	std_ic_t2m_mou_6	std_ic_t2m_mou_7	std_ic_t2m_mou_8	std_ic_t2f_mou_6	std_ic_t2f_mou_7	std_ic_t2f_mou_8	std_ic_mou_6	std_ic_mou_7	std_ic_mou_8	spl_ic_mou_6	spl_ic_mou_7	spl_ic_mou_8	isd_ic_mou_6	isd_ic_mou_7	isd_ic_mou_8	ic_others_6	ic_others_7	ic_others_8	total_rech_num_6	total_rech_num_7	total_rech_num_8	max_rech_amt_6	max_rech_amt_7	max_rech_amt_8	last_day_rch_amt_6	last_day_rch_amt_7	last_day_rch_amt_8	aon	Average_rech_amt_6n7	Churn	delta_vol_2g	delta_vol_3g	delta_total_og_mou	delta_total_ic_mou	delta_vbc_3g	delta_arpu	delta_total_rech_amt	sachet_3g_6_0	sachet_3g_6_1	sachet_3g_6_2	monthly_2g_7_0	monthly_2g_7_1	monthly_2g_7_2	monthly_2g_8_0	monthly_2g_8_1	sachet_3g_8_0	sachet_3g_8_1	monthly_3g_7_0	monthly_3g_7_1	monthly_3g_7_2	sachet_2g_6_0	sachet_2g_6_1	sachet_2g_6_2	sachet_2g_6_3	sachet_2g_6_4	monthly_2g_6_0	monthly_2g_6_1	monthly_2g_6_2	sachet_2g_7_0	sachet_2g_7_1	sachet_2g_7_2	sachet_2g_7_3	sachet_2g_7_4	sachet_2g_7_5	sachet_3g_7_0	sachet_3g_7_1	sachet_3g_7_2	monthly_3g_8_0	monthly_3g_8_1	monthly_3g_8_2	monthly_3g_6_0	monthly_3g_6_1	monthly_3g_6_2	sachet_2g_8_0	sachet_2g_8_1	sachet_2g_8_2	sachet_2g_8_3	sachet_2g_8_4	sachet_2g_8_5
mobile_number
7000701601	57.84	54.68	52.29	453.43	567.16	325.91	16.23	33.49	31.64	23.74	12.59	38.06	51.39	31.38	40.28	308.63	447.38	162.28	62.13	55.14	53.23	0.0	0.0	0.00	422.16	533.91	255.79	4.30	23.29	12.01	49.89	31.76	49.14	6.66	20.08	16.68	60.86	75.14	77.84	0.0	0.18	10.01	4.50	0.00	6.50	0.00	0.0	0.0	58.14	32.26	27.31	217.56	221.49	121.19	152.16	101.46	39.53	427.88	355.23	188.04	36.89	11.83	30.39	91.44	126.99	141.33	52.19	34.24	22.21	180.54	173.08	193.94	0.21	0.0	0.0	2.06	14.53	31.590	15.740	15.19	15.14	5.0	5.0	7.0	1000.0	790.0	951.0	0.0	0.0	619.0	802	1185.0	1	0.00	0.000	-198.225	-163.510	38.680	864.34085	1036.4	1	0	0	1	0	0	1	0	1	0	1	0	0	1	0	0	0	0	1	0	0	1	0	0	0	0	0	1	0	0	1	0	0	1	0	0	1	0	0	0	0	0
7001524846	413.69	351.03	35.08	94.66	80.63	136.48	0.00	0.00	0.00	0.00	0.00	0.00	297.13	217.59	12.49	80.96	70.58	50.54	0.00	0.00	0.00	0.0	0.0	7.15	378.09	288.18	63.04	116.56	133.43	22.58	13.69	10.04	75.69	0.00	0.00	0.00	130.26	143.48	98.28	0.0	0.00	0.00	0.00	0.00	10.23	0.00	0.0	0.0	23.84	9.84	0.31	57.58	13.98	15.48	0.00	0.00	0.00	81.43	23.83	15.79	0.00	0.58	0.10	22.43	4.08	0.65	0.00	0.00	0.00	22.43	4.66	0.75	0.00	0.0	0.0	0.00	0.00	0.000	0.000	0.00	0.00	19.0	21.0	14.0	90.0	154.0	30.0	50.0	0.0	10.0	315	519.0	0	-177.97	-363.535	-298.450	-49.635	-495.375	-298.11000	-399.0	1	0	0	0	1	0	1	0	1	0	1	0	0	1	0	0	0	0	1	0	0	0	1	0	0	0	0	1	0	0	1	0	0	1	0	0	0	0	0	1	0	0
7002191713	501.76	108.39	534.24	413.31	119.28	482.46	23.53	144.24	72.11	7.98	35.26	1.44	49.63	6.19	36.01	151.13	47.28	294.46	4.54	0.00	23.51	0.0	0.0	0.49	205.31	53.48	353.99	446.41	85.98	498.23	255.36	52.94	156.94	0.00	0.00	0.00	701.78	138.93	655.18	0.0	0.00	1.29	0.00	0.00	4.78	0.00	0.0	0.0	67.88	7.58	52.58	142.88	18.53	195.18	4.81	0.00	7.49	215.58	26.11	255.26	115.68	38.29	154.58	308.13	29.79	317.91	0.00	0.00	1.91	423.81	68.09	474.41	0.45	0.0	0.0	239.60	62.11	249.888	20.708	16.24	21.44	6.0	4.0	11.0	110.0	110.0	130.0	110.0	50.0	0.0	2607	380.0	0	0.02	0.000	465.510	573.935	0.000	244.00150	337.0	1	0	0	1	0	0	1	0	1	0	1	0	0	1	0	0	0	0	1	0	0	1	0	0	0	0	0	1	0	0	1	0	0	1	0	0	0	0	0	1	0	0
7000875565	50.51	74.01	70.61	296.29	229.74	162.76	0.00	2.83	0.00	0.00	17.74	0.00	42.61	65.16	67.38	273.29	145.99	128.28	0.00	4.48	10.26	0.0	0.0	0.00	315.91	215.64	205.93	7.89	2.58	3.23	22.99	64.51	18.29	0.00	0.00	0.00	30.89	67.09	21.53	0.0	0.00	0.00	0.00	3.26	5.91	0.00	0.0	0.0	41.33	71.44	28.89	226.81	149.69	150.16	8.71	8.68	32.71	276.86	229.83	211.78	68.79	78.64	6.33	18.68	73.08	73.93	0.51	0.00	2.18	87.99	151.73	82.44	0.00	0.0	0.0	0.00	0.00	0.230	0.000	0.00	0.00	10.0	6.0	2.0	110.0	110.0	130.0	100.0	100.0	130.0	511	459.0	0	0.00	0.000	-83.030	-78.750	-12.170	-177.52800	-299.0	1	0	0	1	0	0	1	0	1	0	1	0	0	1	0	0	0	0	1	0	0	1	0	0	0	0	0	1	0	0	1	0	0	1	0	0	1	0	0	0	0	0
7000187447	1185.91	9.28	7.79	61.64	0.00	5.54	0.00	4.76	4.81	0.00	8.46	13.34	38.99	0.00	0.00	58.54	0.00	0.00	0.00	0.00	0.00	0.0	0.0	0.00	97.54	0.00	0.00	1146.91	0.81	0.00	1.55	0.00	0.00	0.00	0.00	0.00	1148.46	0.81	0.00	0.0	0.00	0.00	2.58	0.00	0.00	0.93	0.0	0.0	34.54	0.00	0.00	47.41	2.31	0.00	0.00	0.00	0.00	81.96	2.31	0.00	8.63	0.00	0.00	1.28	0.00	0.00	0.00	0.00	0.00	9.91	0.00	0.00	0.00	0.0	0.0	0.00	0.00	0.000	0.000	0.00	0.00	19.0	2.0	4.0	110.0	0.0	30.0	30.0	0.0	0.0	667	408.0	0	0.00	0.000	-625.170	-47.095	0.000	-328.99500	-378.0	1	0	0	1	0	0	1	0	1	0	1	0	0	1	0	0	0	0	1	0	0	1	0	0	0	0	0	1	0	0	1	0	0	1	0	0	1	0	0	0	0	0

Train-Test Split

1y = data.pop('Churn') # Predicted / Target Variable
2X = data # Predictor variables

1from sklearn.model_selection import train_test_split
2X_train, X_test, y_train, y_test = train_test_split(X,y, train_size=0.7, random_state=42)

Class Imbalance

1y.value_counts(normalize=True).to_frame()

	Churn
0	0.913598
1	0.086402

1# Ratio of classes 
2class_0 = y[y == 0].count()
3class_1 = y[y == 1].count()
4
5print(f'Class Imbalance Ratio : {round(class_1/class_0,3)}')

1Class Imbalance Ratio : 0.095

To account for class imbalance, Synthetic Minority Class Oversampling Technique (SMOTE) could be used.

Using SMOTE

1#!pip install imblearn
2from imblearn.over_sampling import SMOTE
3smt = SMOTE(random_state=42, k_neighbors=5)
4
5# Resampling Train set to account for class imbalance
6
7X_train_resampled, y_train_resampled= smt.fit_resample(X_train, y_train)
8X_train_resampled.head()

	onnet_mou_6	onnet_mou_7	onnet_mou_8	offnet_mou_6	offnet_mou_7	offnet_mou_8	roam_ic_mou_6	roam_ic_mou_7	roam_ic_mou_8	roam_og_mou_6	roam_og_mou_7	roam_og_mou_8	loc_og_t2t_mou_6	loc_og_t2t_mou_7	loc_og_t2t_mou_8	loc_og_t2m_mou_6	loc_og_t2m_mou_7	loc_og_t2m_mou_8	loc_og_t2f_mou_6	loc_og_t2f_mou_7	loc_og_t2f_mou_8	loc_og_t2c_mou_6	loc_og_t2c_mou_7	loc_og_t2c_mou_8	loc_og_mou_6	loc_og_mou_7	loc_og_mou_8	std_og_t2t_mou_6	std_og_t2t_mou_7	std_og_t2t_mou_8	std_og_t2m_mou_6	std_og_t2m_mou_7	std_og_t2m_mou_8	std_og_t2f_mou_6	std_og_t2f_mou_7	std_og_t2f_mou_8	std_og_mou_6	std_og_mou_7	std_og_mou_8	isd_og_mou_6	isd_og_mou_7	isd_og_mou_8	spl_og_mou_6	spl_og_mou_7	spl_og_mou_8	og_others_6	og_others_7	og_others_8	loc_ic_t2t_mou_6	loc_ic_t2t_mou_7	loc_ic_t2t_mou_8	loc_ic_t2m_mou_6	loc_ic_t2m_mou_7	loc_ic_t2m_mou_8	loc_ic_t2f_mou_6	loc_ic_t2f_mou_7	loc_ic_t2f_mou_8	loc_ic_mou_6	loc_ic_mou_7	loc_ic_mou_8	std_ic_t2t_mou_6	std_ic_t2t_mou_7	std_ic_t2t_mou_8	std_ic_t2m_mou_6	std_ic_t2m_mou_7	std_ic_t2m_mou_8	std_ic_t2f_mou_6	std_ic_t2f_mou_7	std_ic_t2f_mou_8	std_ic_mou_6	std_ic_mou_7	std_ic_mou_8	spl_ic_mou_6	spl_ic_mou_7	spl_ic_mou_8	isd_ic_mou_6	isd_ic_mou_7	isd_ic_mou_8	ic_others_6	ic_others_7	ic_others_8	total_rech_num_6	total_rech_num_7	total_rech_num_8	max_rech_amt_6	max_rech_amt_7	max_rech_amt_8	last_day_rch_amt_6	last_day_rch_amt_7	last_day_rch_amt_8	aon	Average_rech_amt_6n7	delta_vol_2g	delta_vol_3g	delta_total_og_mou	delta_total_ic_mou	delta_vbc_3g	delta_arpu	delta_total_rech_amt	sachet_3g_6_0	sachet_3g_6_1	sachet_3g_6_2	monthly_2g_7_0	monthly_2g_7_1	monthly_2g_7_2	monthly_2g_8_0	monthly_2g_8_1	sachet_3g_8_0	sachet_3g_8_1	monthly_3g_7_0	monthly_3g_7_1	monthly_3g_7_2	sachet_2g_6_0	sachet_2g_6_1	sachet_2g_6_2	sachet_2g_6_3	sachet_2g_6_4	monthly_2g_6_0	monthly_2g_6_1	monthly_2g_6_2	sachet_2g_7_0	sachet_2g_7_1	sachet_2g_7_2	sachet_2g_7_3	sachet_2g_7_4	sachet_2g_7_5	sachet_3g_7_0	sachet_3g_7_1	sachet_3g_7_2	monthly_3g_8_0	monthly_3g_8_1	monthly_3g_8_2	monthly_3g_6_0	monthly_3g_6_1	monthly_3g_6_2	sachet_2g_8_0	sachet_2g_8_1	sachet_2g_8_2	sachet_2g_8_3	sachet_2g_8_4	sachet_2g_8_5
0	53.01	52.64	37.48	316.01	195.74	68.36	0.0	0.0	0.0	0.0	0.0	0.0	53.01	52.64	37.48	282.38	171.64	44.51	31.59	17.38	19.43	0.0	0.0	0.00	366.99	241.68	101.43	0.00	0.00	0.00	0.00	2.11	0.00	2.03	4.59	4.41	2.03	6.71	4.41	0.00	0.0	0.00	0.0	0.0	0.00	0.0	0.0	0.0	18.41	40.79	11.79	292.99	191.98	85.89	6.26	1.21	10.39	317.68	233.99	108.09	0.00	0.00	0.00	0.66	0.00	0.00	5.61	1.53	2.76	6.28	1.53	2.76	0.00	0.0	0.00	0.00	0.00	9.55	0.00	0.00	0.00	6.0	5.0	4.0	198.0	198.0	198.0	110.0	130.0	130.0	1423	483.0	-791.7700	1077.750	-202.870	-159.335	71.085	-172.4995	-155.0	1	0	0	0	1	0	0	1	1	0	1	0	0	1	0	0	0	0	0	1	0	1	0	0	0	0	0	1	0	0	1	0	0	1	0	0	1	0	0	0	0	0
1	91.39	216.14	150.58	504.19	301.98	434.41	0.0	0.0	0.0	0.0	0.0	0.0	40.36	36.21	27.73	37.26	36.73	59.61	0.00	0.00	0.00	0.0	0.0	0.58	77.63	72.94	87.34	51.03	179.93	122.84	465.96	265.24	356.44	0.00	0.00	0.00	516.99	445.18	479.29	0.96	0.0	3.89	0.0	0.0	14.45	0.0	0.0	0.0	104.39	31.98	35.83	154.11	147.88	243.53	0.00	0.76	0.00	258.51	180.63	279.36	4.03	2.99	0.46	6.36	12.31	3.91	0.00	0.00	0.00	10.39	15.31	4.38	0.58	0.0	0.25	19.66	21.96	86.63	0.23	0.56	1.04	8.0	11.0	12.0	110.0	130.0	130.0	0.0	130.0	0.0	189	454.0	0.0000	0.000	28.130	117.745	0.000	48.6160	-94.0	1	0	0	1	0	0	1	0	1	0	1	0	0	1	0	0	0	0	1	0	0	1	0	0	0	0	0	1	0	0	1	0	0	1	0	0	1	0	0	0	0	0
2	11.96	14.13	0.40	1.51	0.00	0.00	0.0	0.0	0.0	0.0	0.0	0.0	11.96	14.13	0.40	1.51	0.00	0.00	0.00	0.00	0.00	0.0	0.0	0.00	13.48	14.13	0.40	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.0	0.00	0.0	0.0	0.00	0.0	0.0	0.0	20.58	20.39	97.66	36.84	21.58	18.66	5.48	0.73	1.43	62.91	42.71	117.76	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.0	0.00	0.00	0.00	0.00	0.00	0.00	0.00	5.0	3.0	4.0	252.0	252.0	252.0	252.0	0.0	252.0	2922	403.0	-44.6300	-5.525	-13.405	64.950	0.000	75.3940	151.0	1	0	0	1	0	0	1	0	1	0	0	1	0	1	0	0	0	0	1	0	0	1	0	0	0	0	0	1	0	0	0	0	1	0	0	1	1	0	0	0	0	0
3	532.66	537.31	738.21	49.03	71.64	39.43	0.0	0.0	0.0	0.0	0.0	0.0	24.46	19.79	37.74	41.26	47.86	39.43	1.19	4.04	0.00	0.0	0.0	0.00	66.93	71.71	77.18	508.19	517.51	700.46	6.56	18.24	0.00	0.00	1.48	0.00	514.76	537.24	700.46	0.00	0.0	0.00	0.0	0.0	0.00	0.0	0.0	0.0	19.86	28.81	20.24	66.08	94.18	67.54	51.74	68.16	50.08	137.69	191.16	137.88	18.83	14.56	1.28	1.08	20.89	6.83	0.00	3.08	3.05	19.91	38.54	11.16	0.00	0.0	0.00	0.00	5.28	7.49	0.00	0.00	0.00	10.0	13.0	12.0	145.0	150.0	145.0	0.0	150.0	0.0	1128	521.0	-10.1500	-108.195	182.315	-39.760	0.000	192.8075	207.0	1	0	0	1	0	0	1	0	1	0	0	1	0	1	0	0	0	0	1	0	0	1	0	0	0	0	0	1	0	0	0	0	1	0	1	0	1	0	0	0	0	0
4	122.68	105.51	149.33	302.23	211.44	264.11	0.0	0.0	0.0	0.0	0.0	0.0	122.68	105.51	149.33	301.04	194.06	257.14	0.00	0.66	0.51	0.0	0.0	0.00	423.73	300.24	406.99	0.00	0.00	0.00	1.18	15.75	6.44	0.00	0.96	0.00	1.18	16.71	6.44	0.00	0.0	0.00	0.0	0.0	0.00	0.0	0.0	0.0	228.54	198.24	231.13	412.99	392.98	353.86	81.76	89.69	88.74	723.31	680.93	673.74	0.00	0.00	1.05	8.14	5.33	0.70	11.83	6.58	10.44	19.98	11.91	12.19	0.00	0.0	0.00	0.43	0.00	0.48	0.00	0.00	0.00	5.0	5.0	4.0	325.0	154.0	164.0	325.0	154.0	164.0	2453	721.0	654.3125	-686.915	42.505	-31.855	-433.700	-55.1110	-105.0	1	0	0	0	0	1	1	0	1	0	1	0	0	1	0	0	0	0	0	1	0	1	0	0	0	0	0	1	0	0	0	0	1	1	0	0	1	0	0	0	0	0

Standardizing Columns

1# columns with numerical data
2condition1 = data.dtypes == 'int'
3condition2 = data.dtypes == 'float'
4numerical_vars = data.columns[condition1 | condition2].to_list()

1# Standard scaling
2from sklearn.preprocessing import StandardScaler
3scaler = StandardScaler() 
4
5# Fit and transform train set 
6X_train_resampled[numerical_vars] = scaler.fit_transform(X_train_resampled[numerical_vars])
7
8# Transform test set
9X_test[numerical_vars] = scaler.transform(X_test[numerical_vars])

1# summary statistics of standardized variables
2round(X_train_resampled.describe(),2)

	onnet_mou_6	onnet_mou_7	onnet_mou_8	offnet_mou_6	offnet_mou_7	offnet_mou_8	roam_ic_mou_6	roam_ic_mou_7	roam_ic_mou_8	roam_og_mou_6	roam_og_mou_7	roam_og_mou_8	loc_og_t2t_mou_6	loc_og_t2t_mou_7	loc_og_t2t_mou_8	loc_og_t2m_mou_6	loc_og_t2m_mou_7	loc_og_t2m_mou_8	loc_og_t2f_mou_6	loc_og_t2f_mou_7	loc_og_t2f_mou_8	loc_og_t2c_mou_6	loc_og_t2c_mou_7	loc_og_t2c_mou_8	loc_og_mou_6	loc_og_mou_7	loc_og_mou_8	std_og_t2t_mou_6	std_og_t2t_mou_7	std_og_t2t_mou_8	std_og_t2m_mou_6	std_og_t2m_mou_7	std_og_t2m_mou_8	std_og_t2f_mou_6	std_og_t2f_mou_7	std_og_t2f_mou_8	std_og_mou_6	std_og_mou_7	std_og_mou_8	isd_og_mou_6	isd_og_mou_7	isd_og_mou_8	spl_og_mou_6	spl_og_mou_7	spl_og_mou_8	og_others_6	og_others_7	og_others_8	loc_ic_t2t_mou_6	loc_ic_t2t_mou_7	loc_ic_t2t_mou_8	loc_ic_t2m_mou_6	loc_ic_t2m_mou_7	loc_ic_t2m_mou_8	loc_ic_t2f_mou_6	loc_ic_t2f_mou_7	loc_ic_t2f_mou_8	loc_ic_mou_6	loc_ic_mou_7	loc_ic_mou_8	std_ic_t2t_mou_6	std_ic_t2t_mou_7	std_ic_t2t_mou_8	std_ic_t2m_mou_6	std_ic_t2m_mou_7	std_ic_t2m_mou_8	std_ic_t2f_mou_6	std_ic_t2f_mou_7	std_ic_t2f_mou_8	std_ic_mou_6	std_ic_mou_7	std_ic_mou_8	spl_ic_mou_6	spl_ic_mou_7	spl_ic_mou_8	isd_ic_mou_6	isd_ic_mou_7	isd_ic_mou_8	ic_others_6	ic_others_7	ic_others_8	total_rech_num_6	total_rech_num_7	total_rech_num_8	max_rech_amt_6	max_rech_amt_7	max_rech_amt_8	last_day_rch_amt_6	last_day_rch_amt_7	last_day_rch_amt_8	aon	Average_rech_amt_6n7	delta_vol_2g	delta_vol_3g	delta_total_og_mou	delta_total_ic_mou	delta_vbc_3g	delta_arpu	delta_total_rech_amt	sachet_3g_6_0	sachet_3g_6_1	sachet_3g_6_2	monthly_2g_7_0	monthly_2g_7_1	monthly_2g_7_2	monthly_2g_8_0	monthly_2g_8_1	sachet_3g_8_0	sachet_3g_8_1	monthly_3g_7_0	monthly_3g_7_1	monthly_3g_7_2	sachet_2g_6_0	sachet_2g_6_1	sachet_2g_6_2	sachet_2g_6_3	sachet_2g_6_4	monthly_2g_6_0	monthly_2g_6_1	monthly_2g_6_2	sachet_2g_7_0	sachet_2g_7_1	sachet_2g_7_2	sachet_2g_7_3	sachet_2g_7_4	sachet_2g_7_5	sachet_3g_7_0	sachet_3g_7_1	sachet_3g_7_2	monthly_3g_8_0	monthly_3g_8_1	monthly_3g_8_2	monthly_3g_6_0	monthly_3g_6_1	monthly_3g_6_2	sachet_2g_8_0	sachet_2g_8_1	sachet_2g_8_2	sachet_2g_8_3	sachet_2g_8_4	sachet_2g_8_5
count	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.0	38374.0	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00	38374.00
mean	-0.00	-0.00	0.00	0.00	-0.00	-0.00	-0.00	-0.00	0.00	-0.00	-0.00	0.00	-0.00	-0.00	0.00	0.00	-0.00	0.00	0.00	-0.00	-0.00	-0.00	0.00	-0.00	0.00	-0.00	-0.00	-0.00	-0.00	-0.00	-0.00	-0.00	0.00	0.00	0.00	0.00	-0.00	0.00	0.00	-0.00	-0.00	0.00	0.00	0.00	0.00	-0.00	0.0	0.0	0.00	-0.00	-0.00	-0.00	0.00	-0.00	0.00	0.00	0.00	-0.00	-0.00	-0.00	0.00	0.00	-0.00	0.00	0.00	0.00	0.00	0.00	-0.00	-0.00	0.00	-0.00	-0.00	-0.00	-0.00	-0.00	0.00	0.00	-0.00	-0.00	0.00	-0.00	0.00	-0.00	-0.00	-0.00	0.00	0.00	-0.00	0.00	0.00	-0.00	0.00	0.00	-0.00	0.00	-0.00	0.00	-0.00	0.00	-0.00	-0.00	-0.00	-0.00	-0.00	0.00	0.00	-0.00	0.00	0.00	0.00	0.00	0.00	-0.00	0.00	0.00	0.00	0.00	0.00	0.00	-0.00	-0.00	-0.00	0.00	0.00	-0.00	-0.00	0.00	-0.00	-0.00	0.00	-0.00	-0.00	-0.00	-0.00	-0.00	-0.00	0.00	-0.00	0.00	0.00
std	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.0	0.0	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
min	-0.73	-0.68	-0.53	-0.94	-0.89	-0.70	-0.31	-0.32	-0.33	-0.33	-0.36	-0.36	-0.50	-0.49	-0.42	-0.75	-0.73	-0.59	-0.38	-0.38	-0.33	-0.37	-0.37	-0.31	-0.76	-0.74	-0.60	-0.57	-0.54	-0.40	-0.60	-0.57	-0.43	-0.22	-0.22	-0.19	-0.79	-0.74	-0.53	-0.20	-0.18	-0.15	-0.51	-0.53	-0.43	-0.44	0.0	0.0	-0.61	-0.57	-0.48	-0.77	-0.75	-0.61	-0.40	-0.39	-0.35	-0.80	-0.77	-0.63	-0.45	-0.43	-0.33	-0.51	-0.47	-0.39	-0.26	-0.26	-0.22	-0.56	-0.52	-0.41	-0.47	-0.21	-0.20	-0.28	-0.27	-0.22	-0.27	-0.25	-0.22	-1.50	-1.37	-1.02	-1.08	-1.04	-0.86	-0.93	-0.85	-0.64	-1.01	-0.91	-28.14	-27.16	-11.65	-14.66	-22.68	-14.96	-14.68	-3.43	-0.16	-0.08	-3.10	-0.25	-0.09	-3.78	-0.23	-4.62	-0.14	-2.78	-0.23	-0.13	-1.95	-0.22	-0.14	-0.11	-0.09	-2.99	-0.24	-0.08	-1.99	-0.21	-0.14	-0.10	-0.09	-0.08	-3.44	-0.16	-0.07	-3.33	-0.22	-0.12	-2.66	-0.23	-0.12	-2.11	-0.23	-0.14	-0.11	-0.10	-0.09
25%	-0.63	-0.60	-0.52	-0.66	-0.65	-0.66	-0.31	-0.32	-0.33	-0.33	-0.36	-0.36	-0.45	-0.45	-0.42	-0.63	-0.63	-0.59	-0.38	-0.38	-0.33	-0.37	-0.37	-0.31	-0.63	-0.63	-0.60	-0.57	-0.54	-0.40	-0.59	-0.56	-0.43	-0.22	-0.22	-0.19	-0.77	-0.72	-0.53	-0.20	-0.18	-0.15	-0.51	-0.53	-0.43	-0.44	0.0	0.0	-0.53	-0.51	-0.48	-0.62	-0.61	-0.61	-0.40	-0.39	-0.35	-0.63	-0.62	-0.63	-0.45	-0.43	-0.33	-0.49	-0.46	-0.39	-0.26	-0.26	-0.22	-0.51	-0.48	-0.41	-0.47	-0.21	-0.20	-0.28	-0.27	-0.22	-0.27	-0.25	-0.22	-0.68	-0.66	-0.63	-0.40	-0.45	-0.70	-0.64	-0.65	-0.64	-0.73	-0.68	0.12	0.11	-0.41	-0.22	0.08	-0.51	-0.48	0.29	-0.16	-0.08	0.32	-0.25	-0.09	0.26	-0.23	0.22	-0.14	0.36	-0.23	-0.13	0.51	-0.22	-0.14	-0.11	-0.09	0.33	-0.24	-0.08	0.50	-0.21	-0.14	-0.10	-0.09	-0.08	0.29	-0.16	-0.07	0.30	-0.22	-0.12	0.38	-0.23	-0.12	0.47	-0.23	-0.14	-0.11	-0.10	-0.09
50%	-0.42	-0.41	-0.40	-0.33	-0.33	-0.36	-0.31	-0.32	-0.33	-0.33	-0.36	-0.36	-0.32	-0.32	-0.35	-0.37	-0.37	-0.43	-0.38	-0.38	-0.33	-0.37	-0.37	-0.31	-0.36	-0.37	-0.43	-0.50	-0.48	-0.40	-0.45	-0.45	-0.41	-0.22	-0.22	-0.19	-0.42	-0.45	-0.49	-0.20	-0.18	-0.15	-0.43	-0.43	-0.43	-0.44	0.0	0.0	-0.34	-0.33	-0.37	-0.34	-0.35	-0.40	-0.36	-0.35	-0.35	-0.34	-0.35	-0.40	-0.38	-0.36	-0.33	-0.34	-0.34	-0.35	-0.26	-0.26	-0.22	-0.33	-0.33	-0.35	-0.47	-0.21	-0.20	-0.28	-0.27	-0.22	-0.27	-0.25	-0.22	-0.25	-0.30	-0.32	-0.33	-0.25	-0.07	-0.16	-0.34	-0.43	-0.39	-0.35	0.15	0.11	0.23	0.13	0.08	0.08	0.03	0.29	-0.16	-0.08	0.32	-0.25	-0.09	0.26	-0.23	0.22	-0.14	0.36	-0.23	-0.13	0.51	-0.22	-0.14	-0.11	-0.09	0.33	-0.24	-0.08	0.50	-0.21	-0.14	-0.10	-0.09	-0.08	0.29	-0.16	-0.07	0.30	-0.22	-0.12	0.38	-0.23	-0.12	0.47	-0.23	-0.14	-0.11	-0.10	-0.09
75%	0.20	0.15	0.01	0.27	0.26	0.23	-0.27	-0.25	-0.22	-0.28	-0.21	-0.20	0.01	0.00	-0.04	0.23	0.22	0.16	-0.13	-0.13	-0.20	-0.24	-0.21	-0.31	0.24	0.24	0.17	0.08	0.01	-0.20	0.10	0.07	-0.10	-0.22	-0.22	-0.19	0.45	0.39	0.07	-0.20	-0.18	-0.15	0.05	0.07	-0.05	-0.11	0.0	0.0	0.09	0.06	0.03	0.20	0.20	0.17	-0.09	-0.11	-0.15	0.23	0.21	0.20	-0.02	-0.04	-0.14	0.02	-0.00	-0.07	-0.25	-0.26	-0.22	0.05	0.03	-0.04	-0.14	-0.21	-0.20	-0.26	-0.26	-0.22	-0.21	-0.23	-0.22	0.37	0.40	0.28	0.06	0.02	0.22	0.14	0.34	0.58	0.39	0.30	0.15	0.11	0.50	0.36	0.08	0.58	0.58	0.29	-0.16	-0.08	0.32	-0.25	-0.09	0.26	-0.23	0.22	-0.14	0.36	-0.23	-0.13	0.51	-0.22	-0.14	-0.11	-0.09	0.33	-0.24	-0.08	0.50	-0.21	-0.14	-0.10	-0.09	-0.08	0.29	-0.16	-0.07	0.30	-0.22	-0.12	0.38	-0.23	-0.12	0.47	-0.23	-0.14	-0.11	-0.10	-0.09
max	4.09	4.46	5.67	4.02	4.45	5.24	6.11	6.09	6.19	5.41	5.44	5.67	7.06	7.45	7.71	5.26	5.34	5.79	7.25	7.30	7.57	6.32	6.47	7.42	5.35	5.53	5.83	4.02	4.36	5.89	4.04	4.64	5.99	8.74	8.89	9.37	3.56	3.93	5.21	7.82	8.52	10.18	6.06	5.90	6.82	5.40	0.0	0.0	6.65	6.93	7.46	5.33	5.53	5.87	7.24	7.12	7.65	5.24	5.53	5.85	6.78	7.35	8.26	6.96	7.26	7.84	8.18	8.35	9.00	6.70	7.11	7.69	4.48	8.02	7.72	7.97	7.96	9.30	8.11	8.48	9.21	4.09	4.28	4.93	5.68	5.62	6.02	5.45	5.54	5.69	3.66	4.46	4.05	4.24	2.96	3.13	4.48	2.84	2.84	0.29	6.28	12.99	0.32	4.07	11.56	0.26	4.32	0.22	7.05	0.36	4.35	7.92	0.51	4.53	7.29	9.20	11.42	0.33	4.12	12.50	0.50	4.78	7.36	9.71	10.80	11.92	0.29	6.43	13.42	0.30	4.57	8.36	0.38	4.28	8.04	0.47	4.29	7.35	9.30	10.13	10.99

Modelling

Model 1 : Interpretable Model : Logistic Regression

Baseline Logistic Regression Model

1from sklearn.linear_model import LogisticRegression
2
3
4baseline_model = LogisticRegression(random_state=100, class_weight='balanced') # `weight of class` balancing technique used
5baseline_model = baseline_model.fit(X_train, y_train)
6
7y_train_pred = baseline_model.predict_proba(X_train)[:,1]
8y_test_pred  = baseline_model.predict_proba(X_test)[:,1]

1y_train_pred = pd.Series(y_train_pred,index = X_train.index, ) # converting test and train to a series to preserve index
2y_test_pred = pd.Series(y_test_pred,index = X_test.index)

Baseline Performance

1# Function for Baseline Performance Metrics
2import math
3def model_metrics(matrix) :
4    TN = matrix[0][0]
5    TP = matrix[1][1]
6    FP = matrix[0][1]
7    FN = matrix[1][0]
8    accuracy = round((TP + TN)/float(TP+TN+FP+FN),3)
9    print('Accuracy :' ,accuracy )
10    sensitivity = round(TP/float(FN + TP),3)
11    print('Sensitivity / True Positive Rate / Recall :', sensitivity)
12    specificity = round(TN/float(TN + FP),3)
13    print('Specificity / True Negative Rate : ', specificity)
14    precision = round(TP/float(TP + FP),3)
15    print('Precision / Positive Predictive Value :', precision)
16    print('F1-score :', round(2*precision*sensitivity/(precision + sensitivity),3))

1# Prediction at threshold of 0.5 
2classification_threshold = 0.5 
3    
4y_train_pred_classified = y_train_pred.map(lambda x : 1 if x > classification_threshold else 0)
5y_test_pred_classified = y_test_pred.map(lambda x : 1 if x > classification_threshold else 0)

1from sklearn.metrics import confusion_matrix
2train_matrix = confusion_matrix(y_train, y_train_pred_classified)
3print('Confusion Matrix for train:\n', train_matrix)
4test_matrix = confusion_matrix(y_test, y_test_pred_classified)
5print('\nConfusion Matrix for test: \n', test_matrix)

1Confusion Matrix for train:
2 [[16001  3186]
3 [  326  1494]]
4
5Confusion Matrix for test: 
6 [[6090 2141]
7 [ 149  624]]

1# Baseline Model Performance : 
2
3print('Train Performance : \n')
4model_metrics(train_matrix)
5
6print('\n\nTest Performance : \n')
7model_metrics(test_matrix)

1Train Performance : 
2
3Accuracy : 0.833
4Sensitivity / True Positive Rate / Recall : 0.821
5Specificity / True Negative Rate :  0.834
6Precision / Positive Predictive Value : 0.319
7F1-score : 0.459
8
9
10Test Performance : 
11
12Accuracy : 0.746
13Sensitivity / True Positive Rate / Recall : 0.807
14Specificity / True Negative Rate :  0.74
15Precision / Positive Predictive Value : 0.226
16F1-score : 0.353

Baseline Performance - Finding Optimum Probability Cutoff

1# Specificity / Sensitivity Tradeoff 
2
3# Classification at probability thresholds between 0 and 1 
4y_train_pred_thres = pd.DataFrame(index=X_train.index)
5thresholds = [float(x)/10 for x in range(10)]
6
7def thresholder(x, thresh) :
8    if x > thresh : 
9        return 1 
10    else : 
11        return 0
12
13    
14for i in thresholds:
15    y_train_pred_thres[i]= y_train_pred.map(lambda x : thresholder(x,i))
16y_train_pred_thres.head()

	0.0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
mobile_number
7000166926	1	1	1	1	1	0	0	0	0	0
7001343085	1	1	1	0	0	0	0	0	0	0
7001863283	1	1	0	0	0	0	0	0	0	0
7002275981	1	1	1	0	0	0	0	0	0	0
7001086221	1	0	0	0	0	0	0	0	0	0

1# # sensitivity, specificity, accuracy for each threshold
2metrics_df = pd.DataFrame(columns=['sensitivity', 'specificity', 'accuracy'])
3
4# Function for calculation of metrics for each threshold
5def model_metrics_thres(matrix) :
6    TN = matrix[0][0]
7    TP = matrix[1][1]
8    FP = matrix[0][1]
9    FN = matrix[1][0]
10    accuracy = round((TP + TN)/float(TP+TN+FP+FN),3)
11    sensitivity = round(TP/float(FN + TP),3)
12    specificity = round(TN/float(TN + FP),3)
13    return sensitivity,specificity,accuracy
14
15# generating a data frame for metrics for each threshold
16for thres,column in zip(thresholds,y_train_pred_thres.columns.to_list()) : 
17    confusion = confusion_matrix(y_train, y_train_pred_thres.loc[:,column])
18    sensitivity,specificity,accuracy = model_metrics_thres(confusion)
19    
20    metrics_df =  metrics_df.append({ 
21        'sensitivity' :sensitivity,
22        'specificity' : specificity,
23        'accuracy' : accuracy
24    }, ignore_index = True)
25    
26metrics_df.index = thresholds
27metrics_df

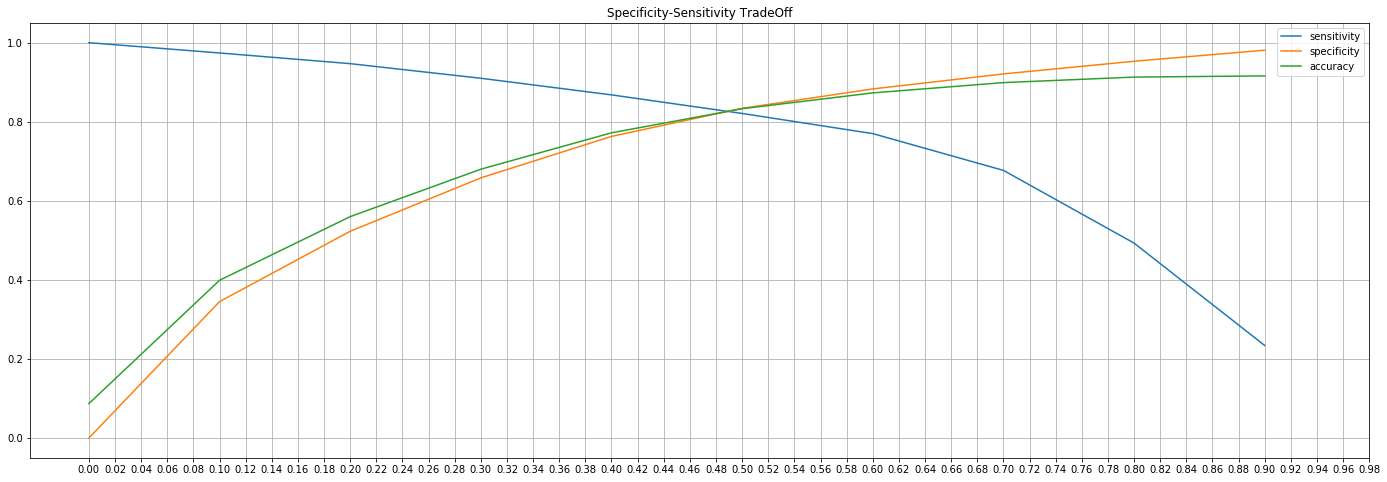
	sensitivity	specificity	accuracy
0.0	1.000	0.000	0.087
0.1	0.974	0.345	0.399
0.2	0.947	0.523	0.560
0.3	0.910	0.658	0.680
0.4	0.868	0.763	0.772
0.5	0.821	0.834	0.833
0.6	0.770	0.883	0.873
0.7	0.677	0.921	0.899
0.8	0.493	0.953	0.913
0.9	0.234	0.981	0.916

1metrics_df.plot(kind='line', figsize=(24,8), grid=True, xticks=np.arange(0,1,0.02),
2                title='Specificity-Sensitivity TradeOff');

Baseline Performance at Optimum Cutoff

1optimum_cutoff = 0.49
2y_train_pred_final = y_train_pred.map(lambda x : 1 if x > optimum_cutoff else 0)
3y_test_pred_final = y_test_pred.map(lambda x : 1 if x > optimum_cutoff else 0)
4
5train_matrix = confusion_matrix(y_train, y_train_pred_final)
6print('Confusion Matrix for train:\n', train_matrix)
7test_matrix = confusion_matrix(y_test, y_test_pred_final)
8print('\nConfusion Matrix for test: \n', test_matrix)

1Confusion Matrix for train:
2 [[15888  3299]
3 [  318  1502]]
4
5Confusion Matrix for test: 
6 [[1329 6902]
7 [  16  757]]

1print('Train Performance: \n')
2model_metrics(train_matrix)
3
4print('\n\nTest Performance : \n')
5model_metrics(test_matrix)

1Train Performance: 
2
3Accuracy : 0.828
4Sensitivity / True Positive Rate / Recall : 0.825
5Specificity / True Negative Rate :  0.828
6Precision / Positive Predictive Value : 0.313
7F1-score : 0.454
8
9
10Test Performance : 
11
12Accuracy : 0.232
13Sensitivity / True Positive Rate / Recall : 0.979
14Specificity / True Negative Rate :  0.161
15Precision / Positive Predictive Value : 0.099
16F1-score : 0.18

1# ROC_AUC score 
2from sklearn.metrics import roc_auc_score
3print('ROC AUC score for Train : ',round(roc_auc_score(y_train, y_train_pred),3), '\n' )
4print('ROC AUC score for Test : ',round(roc_auc_score(y_test, y_test_pred),3) )

1ROC AUC score for Train :  0.891 
2
3ROC AUC score for Test :  0.838

Feature Selection using RFE

1from sklearn.feature_selection import RFE
2from sklearn.linear_model import LogisticRegression
3lr = LogisticRegression(random_state=100 , class_weight='balanced')
4rfe = RFE(lr, 15)
5results = rfe.fit(X_train,y_train)
6results.support_

1array([False, False, False, False, False, False, False, False, False,
2       False, False, False, False, False, False, False, False, False,
3       False, False, False, False, False, False, False, False, False,
4       False, False, False, False, False, False, False, False,  True,
5       False, False, False, False, False, False, False, False, False,
6       False, False, False, False, False, False, False, False, False,
7       False, False,  True, False, False, False, False, False, False,
8       False, False, False, False,  True,  True, False, False, False,
9       False, False, False, False, False, False, False, False, False,
10        True, False,  True, False, False, False, False, False, False,
11       False, False, False, False, False, False, False, False, False,
12        True, False, False,  True, False, False,  True, False, False,
13       False,  True, False, False,  True, False, False, False, False,
14        True, False, False,  True, False, False, False, False, False,
15       False, False, False,  True, False, False, False, False, False,
16        True, False, False, False, False, False])

1# DataFrame with features supported by RFE
2rfe_support = pd.DataFrame({'Column' : X.columns.to_list(), 'Rank' : rfe.ranking_, 
3                                      'Support' :  rfe.support_}).sort_values(by=
4                                       'Rank', ascending=True)
5rfe_support

	Column	Rank	Support
99	sachet_3g_6_0	1	True
120	sachet_2g_7_0	1	True
102	monthly_2g_7_0	1	True
135	sachet_2g_8_0	1	True
81	total_rech_num_6	1	True
129	monthly_3g_8_0	1	True
105	monthly_2g_8_0	1	True
83	total_rech_num_8	1	True
117	monthly_2g_6_0	1	True
68	std_ic_t2f_mou_8	1	True
67	std_ic_t2f_mou_7	1	True
112	sachet_2g_6_0	1	True
109	monthly_3g_7_0	1	True
56	loc_ic_t2f_mou_8	1	True
35	std_og_t2f_mou_8	1	True
40	isd_og_mou_7	2	False
53	loc_ic_t2m_mou_8	3	False
19	loc_og_t2f_mou_7	4	False
62	std_ic_t2t_mou_8	5	False
61	std_ic_t2t_mou_7	6	False
107	sachet_3g_8_0	7	False
41	isd_og_mou_8	8	False
89	last_day_rch_amt_8	9	False
11	roam_og_mou_8	10	False
132	monthly_3g_6_0	11	False
39	isd_og_mou_6	12	False
79	ic_others_7	13	False
50	loc_ic_t2t_mou_8	14	False
7	roam_ic_mou_7	15	False
58	loc_ic_mou_7	16	False
71	std_ic_mou_8	17	False
75	isd_ic_mou_6	18	False
33	std_og_t2f_mou_6	19	False
38	std_og_mou_8	20	False
66	std_ic_t2f_mou_6	21	False
29	std_og_t2t_mou_8	22	False
32	std_og_t2m_mou_8	23	False
78	ic_others_6	24	False
44	spl_og_mou_8	25	False
97	delta_arpu	26	False
85	max_rech_amt_7	27	False
70	std_ic_mou_7	28	False
64	std_ic_t2m_mou_7	29	False
30	std_og_t2m_mou_6	30	False
42	spl_og_mou_6	31	False
27	std_og_t2t_mou_6	32	False
18	loc_og_t2f_mou_6	33	False
60	std_ic_t2t_mou_6	34	False
36	std_og_mou_6	35	False
51	loc_ic_t2m_mou_6	36	False
15	loc_og_t2m_mou_6	37	False
94	delta_total_og_mou	38	False
69	std_ic_mou_6	39	False
65	std_ic_t2m_mou_8	40	False
2	onnet_mou_8	41	False
55	loc_ic_t2f_mou_7	42	False
28	std_og_t2t_mou_7	43	False
13	loc_og_t2t_mou_7	44	False
1	onnet_mou_7	45	False
9	roam_og_mou_6	46	False
21	loc_og_t2c_mou_6	47	False
14	loc_og_t2t_mou_8	48	False
84	max_rech_amt_6	49	False
26	loc_og_mou_8	50	False
8	roam_ic_mou_8	51	False
10	roam_og_mou_7	52	False
48	loc_ic_t2t_mou_6	53	False
57	loc_ic_mou_6	54	False
6	roam_ic_mou_6	55	False
106	monthly_2g_8_1	56	False
87	last_day_rch_amt_6	57	False
49	loc_ic_t2t_mou_7	58	False
98	delta_total_rech_amt	59	False
88	last_day_rch_amt_7	60	False
34	std_og_t2f_mou_7	61	False
126	sachet_3g_7_0	62	False
23	loc_og_t2c_mou_8	63	False
103	monthly_2g_7_1	64	False
118	monthly_2g_6_1	65	False
92	delta_vol_2g	66	False
16	loc_og_t2m_mou_7	67	False
4	offnet_mou_7	68	False
43	spl_og_mou_7	69	False
130	monthly_3g_8_1	70	False
20	loc_og_t2f_mou_8	71	False
17	loc_og_t2m_mou_8	72	False
63	std_ic_t2m_mou_6	73	False
93	delta_vol_3g	74	False
76	isd_ic_mou_7	75	False
24	loc_og_mou_6	76	False
12	loc_og_t2t_mou_6	77	False
54	loc_ic_t2f_mou_6	78	False
0	onnet_mou_6	79	False
3	offnet_mou_6	80	False
77	isd_ic_mou_8	81	False
5	offnet_mou_8	82	False
22	loc_og_t2c_mou_7	83	False
95	delta_total_ic_mou	84	False
52	loc_ic_t2m_mou_7	85	False
59	loc_ic_mou_8	86	False
90	aon	87	False
74	spl_ic_mou_8	88	False
136	sachet_2g_8_1	89	False
121	sachet_2g_7_1	90	False
113	sachet_2g_6_1	91	False
108	sachet_3g_8_1	92	False
80	ic_others_8	93	False
137	sachet_2g_8_2	94	False
138	sachet_2g_8_3	95	False
114	sachet_2g_6_2	96	False
123	sachet_2g_7_3	97	False
133	monthly_3g_6_1	98	False
125	sachet_2g_7_5	99	False
131	monthly_3g_8_2	100	False
119	monthly_2g_6_2	101	False
25	loc_og_mou_7	102	False
104	monthly_2g_7_2	103	False
110	monthly_3g_7_1	104	False
100	sachet_3g_6_1	105	False
139	sachet_2g_8_4	106	False
134	monthly_3g_6_2	107	False
111	monthly_3g_7_2	108	False
37	std_og_mou_7	109	False
31	std_og_t2m_mou_7	110	False
140	sachet_2g_8_5	111	False
101	sachet_3g_6_2	112	False
72	spl_ic_mou_6	113	False
86	max_rech_amt_8	114	False
73	spl_ic_mou_7	115	False
96	delta_vbc_3g	116	False
82	total_rech_num_7	117	False
115	sachet_2g_6_3	118	False
124	sachet_2g_7_4	119	False
127	sachet_3g_7_1	120	False
91	Average_rech_amt_6n7	121	False
45	og_others_6	122	False
116	sachet_2g_6_4	123	False
128	sachet_3g_7_2	124	False
122	sachet_2g_7_2	125	False
47	og_others_8	126	False
46	og_others_7	127	False

1# RFE Selected columns
2rfe_selected_columns = rfe_support.loc[rfe_support['Rank'] == 1,'Column'].to_list()
3rfe_selected_columns

1['sachet_3g_6_0',
2 'sachet_2g_7_0',
3 'monthly_2g_7_0',
4 'sachet_2g_8_0',
5 'total_rech_num_6',
6 'monthly_3g_8_0',
7 'monthly_2g_8_0',
8 'total_rech_num_8',
9 'monthly_2g_6_0',
10 'std_ic_t2f_mou_8',
11 'std_ic_t2f_mou_7',
12 'sachet_2g_6_0',
13 'monthly_3g_7_0',
14 'loc_ic_t2f_mou_8',
15 'std_og_t2f_mou_8']

Logistic Regression with RFE Selected Columns

Model I

1# Logistic Regression Model with RFE columns
2import statsmodels.api as sm 
3
4# Note that the SMOTE resampled Train set is used with statsmodels.api.GLM since it doesnot support class_weight
5logr = sm.GLM(y_train_resampled,(sm.add_constant(X_train_resampled[rfe_selected_columns])), family = sm.families.Binomial())
6logr_fit = logr.fit()
7logr_fit.summary()

Generalized Linear Model Regression Results
Dep. Variable:	Churn	No. Observations:	38374
Model:	GLM	Df Residuals:	38358
Model Family:	Binomial	Df Model:	15
Link Function:	logit	Scale:	1.0000
Method:	IRLS	Log-Likelihood:	-19485.
Date:	Mon, 30 Nov 2020	Deviance:	38969.
Time:	21:57:09	Pearson chi2:	2.80e+05
No. Iterations:	7
Covariance Type:	nonrobust

	coef	std err	z	P>\|z\|	[0.025	0.975]
const	-0.2334	0.015	-15.657	0.000	-0.263	-0.204
sachet_3g_6_0	-0.0396	0.014	-2.886	0.004	-0.066	-0.013
sachet_2g_7_0	-0.0980	0.016	-6.201	0.000	-0.129	-0.067
monthly_2g_7_0	0.0096	0.016	0.594	0.552	-0.022	0.041
sachet_2g_8_0	0.0489	0.015	3.359	0.001	0.020	0.077
total_rech_num_6	0.6047	0.017	35.547	0.000	0.571	0.638
monthly_3g_8_0	0.3993	0.017	23.439	0.000	0.366	0.433
monthly_2g_8_0	0.3697	0.018	21.100	0.000	0.335	0.404
total_rech_num_8	-1.2013	0.019	-62.378	0.000	-1.239	-1.164
monthly_2g_6_0	-0.0194	0.015	-1.262	0.207	-0.050	0.011
std_ic_t2f_mou_8	-0.3364	0.026	-12.792	0.000	-0.388	-0.285
std_ic_t2f_mou_7	0.1535	0.019	8.148	0.000	0.117	0.190
sachet_2g_6_0	-0.1117	0.016	-6.847	0.000	-0.144	-0.080
monthly_3g_7_0	-0.2094	0.017	-12.602	0.000	-0.242	-0.177
loc_ic_t2f_mou_8	-1.2743	0.038	-33.599	0.000	-1.349	-1.200
std_og_t2f_mou_8	-0.2476	0.021	-11.621	0.000	-0.289	-0.206

Logistic Regression with Manual Feature Elimination

1# Using P-value and vif for manual feature elimination
2
3from statsmodels.stats.outliers_influence import variance_inflation_factor
4def vif(X_train_resampled, logr_fit, selected_columns) : 
5    vif = pd.DataFrame()
6    vif['Features'] = rfe_selected_columns
7    vif['VIF'] = [variance_inflation_factor(X_train_resampled[selected_columns].values, i) for i in range(X_train_resampled[selected_columns].shape[1])]
8    vif['VIF'] = round(vif['VIF'], 2)
9    vif = vif.set_index('Features')
10    vif['P-value'] = round(logr_fit.pvalues,4)
11    vif = vif.sort_values(by = ["VIF",'P-value'], ascending = [False,False])
12    return vif
13
14vif(X_train_resampled, logr_fit, rfe_selected_columns)

	VIF	P-value
Features
std_ic_t2f_mou_8	1.66	0.0000
sachet_2g_6_0	1.64	0.0000
sachet_2g_7_0	1.57	0.0000
std_ic_t2f_mou_7	1.56	0.0000
monthly_2g_7_0	1.54	0.5524
monthly_3g_7_0	1.54	0.0000
monthly_3g_8_0	1.52	0.0000
monthly_2g_8_0	1.43	0.0000
monthly_2g_6_0	1.38	0.2069
sachet_2g_8_0	1.36	0.0008
total_rech_num_6	1.27	0.0000
total_rech_num_8	1.25	0.0000
std_og_t2f_mou_8	1.20	0.0000
sachet_3g_6_0	1.12	0.0039
loc_ic_t2f_mou_8	1.09	0.0000

‘monthly_2g_7_0’ has the very p-value. Hence, this feature could be eliminated

1selected_columns = rfe_selected_columns
2selected_columns.remove('monthly_2g_7_0')
3selected_columns

1['sachet_3g_6_0',
2 'sachet_2g_7_0',
3 'sachet_2g_8_0',
4 'total_rech_num_6',
5 'monthly_3g_8_0',
6 'monthly_2g_8_0',
7 'total_rech_num_8',
8 'monthly_2g_6_0',
9 'std_ic_t2f_mou_8',
10 'std_ic_t2f_mou_7',
11 'sachet_2g_6_0',
12 'monthly_3g_7_0',
13 'loc_ic_t2f_mou_8',
14 'std_og_t2f_mou_8']

Model II

1logr2 = sm.GLM(y_train_resampled,(sm.add_constant(X_train_resampled[selected_columns])), family = sm.families.Binomial())
2logr2_fit = logr2.fit()
3logr2_fit.summary()

Generalized Linear Model Regression Results
Dep. Variable:	Churn	No. Observations:	38374
Model:	GLM	Df Residuals:	38359
Model Family:	Binomial	Df Model:	14
Link Function:	logit	Scale:	1.0000
Method:	IRLS	Log-Likelihood:	-19485.
Date:	Mon, 30 Nov 2020	Deviance:	38970.
Time:	21:57:09	Pearson chi2:	2.80e+05
No. Iterations:	7
Covariance Type:	nonrobust

	coef	std err	z	P>\|z\|	[0.025	0.975]
const	-0.2335	0.015	-15.662	0.000	-0.263	-0.204
sachet_3g_6_0	-0.0395	0.014	-2.881	0.004	-0.066	-0.013
sachet_2g_7_0	-0.0982	0.016	-6.217	0.000	-0.129	-0.067
sachet_2g_8_0	0.0491	0.015	3.372	0.001	0.021	0.078
total_rech_num_6	0.6049	0.017	35.566	0.000	0.572	0.638
monthly_3g_8_0	0.4000	0.017	23.521	0.000	0.367	0.433
monthly_2g_8_0	0.3733	0.016	22.696	0.000	0.341	0.406
total_rech_num_8	-1.2012	0.019	-62.375	0.000	-1.239	-1.163
monthly_2g_6_0	-0.0163	0.014	-1.128	0.259	-0.045	0.012
std_ic_t2f_mou_8	-0.3361	0.026	-12.784	0.000	-0.388	-0.285
std_ic_t2f_mou_7	0.1532	0.019	8.136	0.000	0.116	0.190
sachet_2g_6_0	-0.1111	0.016	-6.823	0.000	-0.143	-0.079
monthly_3g_7_0	-0.2098	0.017	-12.633	0.000	-0.242	-0.177
loc_ic_t2f_mou_8	-1.2749	0.038	-33.622	0.000	-1.349	-1.201
std_og_t2f_mou_8	-0.2476	0.021	-11.620	0.000	-0.289	-0.206

1# vif and p-values
2vif(X_train_resampled, logr2_fit, selected_columns)

	VIF	P-value
Features
std_ic_t2f_mou_8	1.66	0.0000
sachet_2g_6_0	1.63	0.0000
sachet_2g_7_0	1.57	0.0000
std_ic_t2f_mou_7	1.56	0.0000
monthly_3g_7_0	1.54	0.0000
monthly_3g_8_0	1.52	0.0000
sachet_2g_8_0	1.36	0.0007
total_rech_num_6	1.27	0.0000
total_rech_num_8	1.25	0.0000
monthly_2g_8_0	1.23	0.0000
monthly_2g_6_0	1.21	0.2595
std_og_t2f_mou_8	1.20	0.0000
sachet_3g_6_0	1.12	0.0040
loc_ic_t2f_mou_8	1.09	0.0000

‘monthly_2g_6_0’ has very high p-value. Hence, this feature could be eliminated

1selected_columns.remove('monthly_2g_6_0')
2selected_columns

1['sachet_3g_6_0',
2 'sachet_2g_7_0',
3 'sachet_2g_8_0',
4 'total_rech_num_6',
5 'monthly_3g_8_0',
6 'monthly_2g_8_0',
7 'total_rech_num_8',
8 'std_ic_t2f_mou_8',
9 'std_ic_t2f_mou_7',
10 'sachet_2g_6_0',
11 'monthly_3g_7_0',
12 'loc_ic_t2f_mou_8',
13 'std_og_t2f_mou_8']

Model III

1logr3 = sm.GLM(y_train_resampled,(sm.add_constant(X_train_resampled[selected_columns])), family = sm.families.Binomial())
2logr3_fit = logr3.fit()
3logr3_fit.summary()

Generalized Linear Model Regression Results
Dep. Variable:	Churn	No. Observations:	38374
Model:	GLM	Df Residuals:	38360
Model Family:	Binomial	Df Model:	13
Link Function:	logit	Scale:	1.0000
Method:	IRLS	Log-Likelihood:	-19486.
Date:	Mon, 30 Nov 2020	Deviance:	38971.
Time:	21:57:10	Pearson chi2:	2.79e+05
No. Iterations:	7
Covariance Type:	nonrobust

	coef	std err	z	P>\|z\|	[0.025	0.975]
const	-0.2336	0.015	-15.667	0.000	-0.263	-0.204
sachet_3g_6_0	-0.0399	0.014	-2.916	0.004	-0.067	-0.013
sachet_2g_7_0	-0.0987	0.016	-6.249	0.000	-0.130	-0.068
sachet_2g_8_0	0.0488	0.015	3.354	0.001	0.020	0.077
total_rech_num_6	0.6053	0.017	35.581	0.000	0.572	0.639
monthly_3g_8_0	0.3994	0.017	23.494	0.000	0.366	0.433
monthly_2g_8_0	0.3666	0.015	23.953	0.000	0.337	0.397
total_rech_num_8	-1.2033	0.019	-62.720	0.000	-1.241	-1.166
std_ic_t2f_mou_8	-0.3363	0.026	-12.788	0.000	-0.388	-0.285
std_ic_t2f_mou_7	0.1532	0.019	8.137	0.000	0.116	0.190
sachet_2g_6_0	-0.1108	0.016	-6.810	0.000	-0.143	-0.079
monthly_3g_7_0	-0.2099	0.017	-12.640	0.000	-0.242	-0.177
loc_ic_t2f_mou_8	-1.2736	0.038	-33.621	0.000	-1.348	-1.199
std_og_t2f_mou_8	-0.2474	0.021	-11.617	0.000	-0.289	-0.206

1# vif and p-values
2vif(X_train_resampled, logr3_fit, selected_columns)

	VIF	P-value
Features
std_ic_t2f_mou_8	1.66	0.0000
sachet_2g_6_0	1.63	0.0000
sachet_2g_7_0	1.57	0.0000
std_ic_t2f_mou_7	1.56	0.0000
monthly_3g_7_0	1.54	0.0000
monthly_3g_8_0	1.52	0.0000
sachet_2g_8_0	1.36	0.0008
total_rech_num_6	1.27	0.0000
total_rech_num_8	1.24	0.0000
std_og_t2f_mou_8	1.20	0.0000
sachet_3g_6_0	1.12	0.0035
loc_ic_t2f_mou_8	1.09	0.0000
monthly_2g_8_0	1.03	0.0000

All features have low p-values(<0.05) and VIF (<5)
This model could be used as the interpretable logistic regression model.

Final Logistic Regression Model with RFE and Manual Elimination

1logr3_fit.summary()

Generalized Linear Model Regression Results
Dep. Variable:	Churn	No. Observations:	38374
Model:	GLM	Df Residuals:	38360
Model Family:	Binomial	Df Model:	13
Link Function:	logit	Scale:	1.0000
Method:	IRLS	Log-Likelihood:	-19486.
Date:	Mon, 30 Nov 2020	Deviance:	38971.
Time:	21:57:10	Pearson chi2:	2.79e+05
No. Iterations:	7
Covariance Type:	nonrobust

	coef	std err	z	P>\|z\|	[0.025	0.975]
const	-0.2336	0.015	-15.667	0.000	-0.263	-0.204
sachet_3g_6_0	-0.0399	0.014	-2.916	0.004	-0.067	-0.013
sachet_2g_7_0	-0.0987	0.016	-6.249	0.000	-0.130	-0.068
sachet_2g_8_0	0.0488	0.015	3.354	0.001	0.020	0.077
total_rech_num_6	0.6053	0.017	35.581	0.000	0.572	0.639
monthly_3g_8_0	0.3994	0.017	23.494	0.000	0.366	0.433
monthly_2g_8_0	0.3666	0.015	23.953	0.000	0.337	0.397
total_rech_num_8	-1.2033	0.019	-62.720	0.000	-1.241	-1.166
std_ic_t2f_mou_8	-0.3363	0.026	-12.788	0.000	-0.388	-0.285
std_ic_t2f_mou_7	0.1532	0.019	8.137	0.000	0.116	0.190
sachet_2g_6_0	-0.1108	0.016	-6.810	0.000	-0.143	-0.079
monthly_3g_7_0	-0.2099	0.017	-12.640	0.000	-0.242	-0.177
loc_ic_t2f_mou_8	-1.2736	0.038	-33.621	0.000	-1.348	-1.199
std_og_t2f_mou_8	-0.2474	0.021	-11.617	0.000	-0.289	-0.206

1selected_columns

1['sachet_3g_6_0',
2 'sachet_2g_7_0',
3 'sachet_2g_8_0',
4 'total_rech_num_6',
5 'monthly_3g_8_0',
6 'monthly_2g_8_0',
7 'total_rech_num_8',
8 'std_ic_t2f_mou_8',
9 'std_ic_t2f_mou_7',
10 'sachet_2g_6_0',
11 'monthly_3g_7_0',
12 'loc_ic_t2f_mou_8',
13 'std_og_t2f_mou_8']

1# Prediction 
2y_train_pred_lr = logr3_fit.predict(sm.add_constant(X_train_resampled[selected_columns]))
3y_train_pred_lr.head()

10    0.118916
21    0.343873
32    0.381230
43    0.015277
54    0.001595
6dtype: float64

1y_test_pred_lr = logr3_fit.predict(sm.add_constant(X_test[selected_columns]))
2y_test_pred_lr.head()

1mobile_number
27002242818    0.013556
37000517161    0.903162
47002162382    0.247123
57002152271    0.330787
67002058655    0.056105
7dtype: float64

Performance

Finding Optimum Probability Cutoff

1# Specificity / Sensitivity Tradeoff 
2
3# Classification at probability thresholds between 0 and 1 
4y_train_pred_thres = pd.DataFrame(index=X_train_resampled.index)
5thresholds = [float(x)/10 for x in range(10)]
6
7def thresholder(x, thresh) :
8    if x > thresh : 
9        return 1 
10    else : 
11        return 0
12
13    
14for i in thresholds:
15    y_train_pred_thres[i]= y_train_pred_lr.map(lambda x : thresholder(x,i))
16y_train_pred_thres.head()

	0.0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
0	1	1	0	0	0	0	0	0	0	0
1	1	1	1	1	0	0	0	0	0	0
2	1	1	1	1	0	0	0	0	0	0
3	1	0	0	0	0	0	0	0	0	0
4	1	0	0	0	0	0	0	0	0	0

1# DataFrame for Performance metrics at each threshold
2
3logr_metrics_df = pd.DataFrame(columns=['sensitivity', 'specificity', 'accuracy'])
4for thres,column in zip(thresholds,y_train_pred_thres.columns.to_list()) : 
5    confusion = confusion_matrix(y_train_resampled, y_train_pred_thres.loc[:,column])
6    sensitivity,specificity,accuracy = model_metrics_thres(confusion)
7    logr_metrics_df =  logr_metrics_df.append({ 
8        'sensitivity' :sensitivity,
9        'specificity' : specificity,
10        'accuracy' : accuracy
11    }, ignore_index = True)
12    
13logr_metrics_df.index = thresholds
14logr_metrics_df

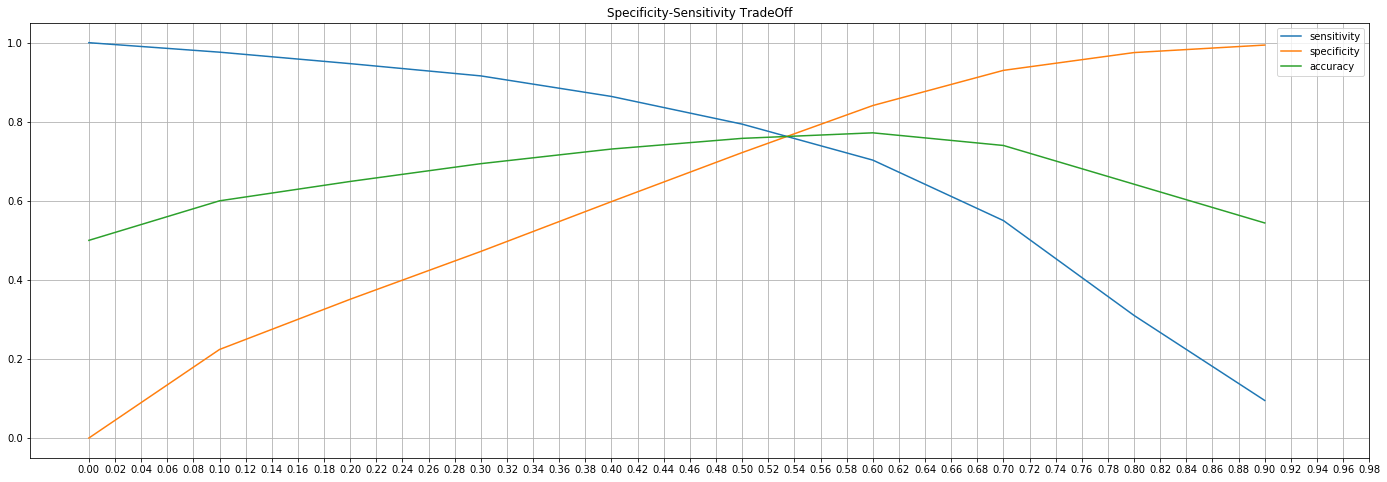
	sensitivity	specificity	accuracy
0.0	1.000	0.000	0.500
0.1	0.976	0.224	0.600
0.2	0.947	0.351	0.649
0.3	0.916	0.472	0.694
0.4	0.864	0.598	0.731
0.5	0.794	0.722	0.758
0.6	0.703	0.841	0.772
0.7	0.550	0.930	0.740
0.8	0.310	0.975	0.642
0.9	0.095	0.994	0.544

1logr_metrics_df.plot(kind='line', figsize=(24,8), grid=True, xticks=np.arange(0,1,0.02),
2                title='Specificity-Sensitivity TradeOff');

The optimum probability cutoff for Logistic regression model is 0.53

1optimum_cutoff = 0.53
2y_train_pred_lr_final = y_train_pred_lr.map(lambda x : 1 if x > optimum_cutoff else 0)
3y_test_pred_lr_final = y_test_pred_lr.map(lambda x : 1 if x > optimum_cutoff else 0)
4
5train_matrix = confusion_matrix(y_train_resampled, y_train_pred_lr_final)
6print('Confusion Matrix for train:\n', train_matrix)
7test_matrix = confusion_matrix(y_test, y_test_pred_lr_final)
8print('\nConfusion Matrix for test: \n', test_matrix)

1Confusion Matrix for train:
2 [[14531  4656]
3 [ 4411 14776]]
4
5Confusion Matrix for test: 
6 [[6313 1918]
7 [ 191  582]]

1print('Train Performance: \n')
2model_metrics(train_matrix)
3
4print('\n\nTest Performance : \n')
5model_metrics(test_matrix)

1Train Performance: 
2
3Accuracy : 0.764
4Sensitivity / True Positive Rate / Recall : 0.77
5Specificity / True Negative Rate :  0.757
6Precision / Positive Predictive Value : 0.76
7F1-score : 0.765
8
9
10Test Performance : 
11
12Accuracy : 0.766
13Sensitivity / True Positive Rate / Recall : 0.753
14Specificity / True Negative Rate :  0.767
15Precision / Positive Predictive Value : 0.233
16F1-score : 0.356

1# ROC_AUC score 
2print('ROC AUC score for Train : ',round(roc_auc_score(y_train_resampled, y_train_pred_lr),3), '\n' )
3print('ROC AUC score for Test : ',round(roc_auc_score(y_test, y_test_pred_lr),3) )

1ROC AUC score for Train :  0.843 
2
3ROC AUC score for Test :  0.828

Model 1 : Logistic Regression (Interpretable Model Summary)

1lr_summary_html = logr3_fit.summary().tables[1].as_html()
2lr_results = pd.read_html(lr_summary_html, header=0, index_col=0)[0]
3coef_column = lr_results.columns[0]
4print('Most important predictors of Churn , in order of importance and their coefficients are as follows : \n')
5lr_results.sort_values(by=coef_column, key=lambda x: abs(x), ascending=False)['coef']

1Most important predictors of Churn , in order of importance and their coefficients are as follows : 
2
3
4
5
6
7
8loc_ic_t2f_mou_8   -1.2736
9total_rech_num_8   -1.2033
10total_rech_num_6    0.6053
11monthly_3g_8_0      0.3994
12monthly_2g_8_0      0.3666
13std_ic_t2f_mou_8   -0.3363
14std_og_t2f_mou_8   -0.2474
15const              -0.2336
16monthly_3g_7_0     -0.2099
17std_ic_t2f_mou_7    0.1532
18sachet_2g_6_0      -0.1108
19sachet_2g_7_0      -0.0987
20sachet_2g_8_0       0.0488
21sachet_3g_6_0      -0.0399
22Name: coef, dtype: float64

The above model could be used as the interpretable model for predicting telecom churn.

PCA

1from sklearn.decomposition import PCA 
2pca = PCA(random_state = 42) 
3pca.fit(X_train) # note that pca is fit on original train set instead of resampled train set. 
4pca.components_

1array([[ 1.64887430e-01,  1.93987506e-01,  1.67239205e-01, ...,
2         1.43967238e-06, -1.55704675e-06, -1.88892194e-06],
3       [ 6.48591961e-02,  9.55966684e-02,  1.20775174e-01, ...,
4        -2.12841595e-06, -1.47944145e-06, -3.90881587e-07],
5       [ 2.38415388e-01,  2.73645507e-01,  2.38436263e-01, ...,
6        -1.25598531e-06, -4.37900299e-07,  6.19889336e-07],
7       ...,
8       [ 1.68015588e-06,  1.93600851e-06, -1.82065762e-06, ...,
9         4.25473944e-03,  2.56738368e-03,  3.51118176e-03],
10       [ 0.00000000e+00, -1.11533905e-16,  1.57807487e-16, ...,
11         1.73764144e-15,  6.22907679e-16,  1.45339158e-16],
12       [ 0.00000000e+00,  4.98537742e-16, -6.02718139e-16, ...,
13         1.27514583e-15,  1.25772226e-15,  3.41773342e-16]])

1pca.explained_variance_ratio_

1array([2.72067612e-01, 1.62438240e-01, 1.20827535e-01, 1.06070063e-01,
2       9.11349433e-02, 4.77504400e-02, 2.63978655e-02, 2.56843982e-02,
3       1.91789343e-02, 1.68045932e-02, 1.55523468e-02, 1.31676589e-02,
4       1.04552128e-02, 7.72970448e-03, 7.22746863e-03, 6.14494838e-03,
5       5.62073089e-03, 5.44579273e-03, 4.59009989e-03, 4.38488162e-03,
6       3.46703626e-03, 3.27941490e-03, 2.78099200e-03, 2.13444270e-03,
7       2.07542043e-03, 1.89794720e-03, 1.41383936e-03, 1.30240760e-03,
8       1.15369576e-03, 1.05262500e-03, 9.64293417e-04, 9.16686049e-04,
9       8.84067044e-04, 7.62966236e-04, 6.61794767e-04, 5.69667265e-04,
10       5.12585166e-04, 5.04441248e-04, 4.82396680e-04, 4.46889495e-04,
11       4.36441254e-04, 4.10389488e-04, 3.51844810e-04, 3.12626195e-04,
12       2.51673027e-04, 2.34723896e-04, 1.96950034e-04, 1.71296745e-04,
13       1.59882693e-04, 1.48330353e-04, 1.45919483e-04, 1.08583729e-04,
14       1.04038518e-04, 8.90621848e-05, 8.53009223e-05, 7.60704088e-05,
15       7.57150133e-05, 6.16615717e-05, 6.07777411e-05, 5.70517541e-05,
16       5.36161089e-05, 5.28495367e-05, 5.14887086e-05, 4.73768570e-05,
17       4.71283394e-05, 4.11523975e-05, 4.10392906e-05, 2.86090257e-05,
18       2.19793282e-05, 1.58203581e-05, 1.50969788e-05, 1.42865579e-05,
19       1.34537530e-05, 1.33026062e-05, 1.10239870e-05, 8.27539516e-06,
20       7.55845974e-06, 6.45372276e-06, 6.22570067e-06, 3.42288900e-06,
21       3.20804681e-06, 3.09270863e-06, 2.86608967e-06, 2.44898003e-06,
22       2.08230568e-06, 1.85144734e-06, 1.64714248e-06, 1.45630245e-06,
23       1.35265729e-06, 1.05472047e-06, 9.89133015e-07, 8.65864423e-07,
24       7.45065121e-07, 3.66727807e-07, 6.49277820e-08, 6.13357428e-08,
25       4.35995018e-08, 2.28152900e-08, 2.00441141e-08, 1.84235145e-08,
26       1.66102335e-08, 1.47870989e-08, 1.23390691e-08, 1.12094165e-08,
27       1.09702422e-08, 9.51924270e-09, 8.61596309e-09, 7.38051070e-09,
28       7.15370081e-09, 6.29095319e-09, 5.00739371e-09, 4.68791660e-09,
29       4.23376173e-09, 4.04558169e-09, 3.75847771e-09, 3.71213838e-09,
30       3.32806929e-09, 3.23527525e-09, 3.12734302e-09, 2.82062311e-09,
31       2.72602311e-09, 2.66103741e-09, 2.46562734e-09, 2.20243536e-09,
32       2.15044476e-09, 1.59498492e-09, 1.47087974e-09, 1.06159357e-09,
33       9.33938436e-10, 8.10080735e-10, 8.04656028e-10, 6.12994365e-10,
34       4.82074297e-10, 4.02577318e-10, 3.58059984e-10, 3.28374076e-10,
35       3.03687605e-10, 7.12091816e-11, 6.13978255e-11, 1.04375208e-33,
36       1.04375208e-33])

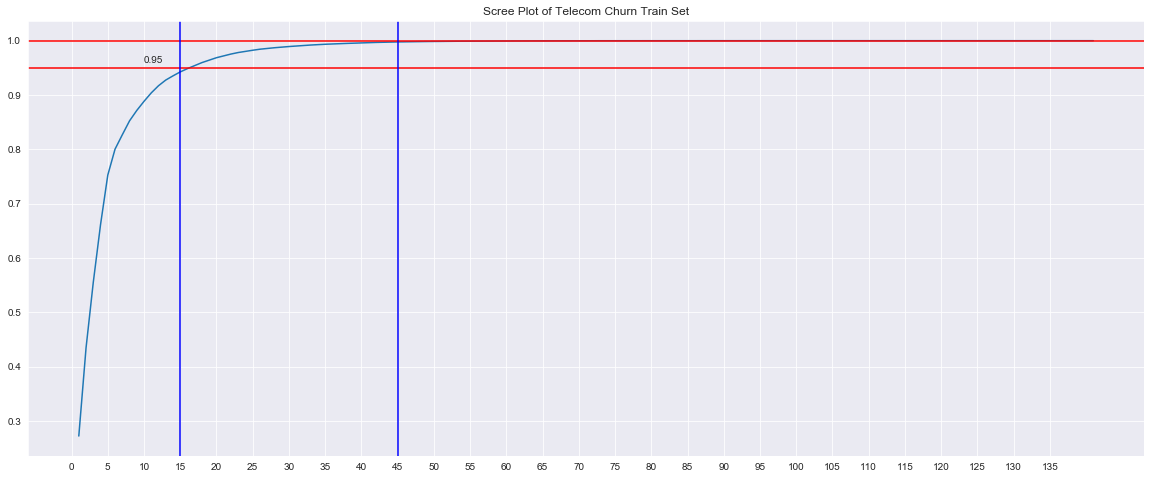
Scree Plot

1var_cum = np.cumsum(pca.explained_variance_ratio_)
2plt.figure(figsize=(20,8))
3sns.set_style('darkgrid')
4sns.lineplot(np.arange(1,len(var_cum) + 1), var_cum)
5plt.xticks(np.arange(0,140,5))
6plt.axhline(0.95,color='r')
7plt.axhline(1.0,color='r')
8plt.axvline(15,color='b')
9plt.axvline(45,color='b')
10plt.text(10,0.96,'0.95')
11
12plt.title('Scree Plot of Telecom Churn Train Set');

From the above scree plot, it is clear that 95% of variance in the train set can be explained by first 16 principal components and 100% of variance is explained by the first 45 principal components.

1# Perform PCA using the first 45 components
2pca_final = PCA(n_components=45, random_state=42)
3transformed_data = pca_final.fit_transform(X_train)
4X_train_pca = pd.DataFrame(transformed_data, columns=["PC_"+str(x) for x in range(1,46)], index = X_train.index)
5data_train_pca = pd.concat([X_train_pca, y_train], axis=1)
6
7data_train_pca.head()

	PC_1	PC_2	PC_3	PC_4	PC_5	PC_6	PC_7	PC_8	PC_9	PC_10	PC_11	PC_12	PC_13	PC_14	PC_15	PC_16	PC_17	PC_18	PC_19	PC_20	PC_21	PC_22	PC_23	PC_24	PC_25	PC_26	PC_27	PC_28	PC_29	PC_30	PC_31	PC_32	PC_33	PC_34	PC_35	PC_36	PC_37	PC_38	PC_39	PC_40	PC_41	PC_42	PC_43	PC_44	PC_45	Churn
mobile_number
7000166926	-907.572208	-342.923676	13.094442	58.813506	-95.616159	-1050.535219	254.648987	-31.445039	305.140339	-216.814250	95.825021	231.408291	-111.002572	-2.007256	444.977249	31.541681	573.831941	-278.539708	30.768637	-36.915195	-0.293915	-83.574447	-13.960479	-60.930941	-53.208613	56.049658	-17.776675	-12.624526	14.149393	-30.559156	26.064776	-1.080160	-19.814893	-3.293546	-2.717923	7.470255	22.686838	28.696686	-14.312037	4.959030	-8.652543	2.473147	17.080399	-21.824778	-8.062901	0
7001343085	573.898045	-902.385767	-424.839214	-331.153508	-148.987005	-36.955710	-134.445130	265.325388	-92.070929	-164.203586	25.105150	-36.980621	164.785936	-222.908959	-12.573878	-50.569424	-44.767869	-62.984835	-18.100729	-86.239469	-115.399141	-45.776518	16.345395	-21.497140	-10.541281	-71.754047	29.230830	-20.880178	-0.690183	3.220864	-21.223298	65.500636	-39.719437	50.424623	10.586150	43.055219	0.209259	-66.107880	13.583016	25.823444	52.037618	-3.272773	8.493995	19.449057	-38.779466	0
7001863283	-1538.198366	514.032564	846.865497	57.032319	-1126.228705	-84.209511	-44.422495	-88.158881	-58.411887	50.518811	3.052703	-229.100202	-109.215465	-3.253782	7.045279	-85.645393	54.536446	-52.292779	20.978943	-90.806167	96.348659	24.280381	-52.425262	42.430049	-40.627473	-12.715890	-4.331719	-4.092290	50.339358	-0.777645	-35.146663	-121.580965	98.868473	-34.068010	-8.941074	22.920757	1.669933	52.644942	-8.542762	9.087643	-18.403853	3.672076	26.073078	27.246371	19.603368	0
7002275981	486.830772	-224.929803	1130.460535	-496.189015	6.009139	81.106845	-148.667431	170.280911	-7.375197	-99.556793	-159.659135	-14.186219	-98.682096	213.233743	-34.920639	-17.212430	29.644778	4.941994	2.799763	-49.580528	-88.567855	16.809461	-9.471018	4.383889	29.532189	38.211558	32.465761	-5.316497	-60.149577	12.593305	20.988200	80.709846	-50.975160	-3.712583	65.002407	-57.837280	-8.312631	-5.931175	-5.053131	-5.667538	-12.102225	-14.690148	-32.215573	12.517731	-20.158820	0
7001086221	-1420.949314	794.071749	99.221352	155.118564	145.349456	784.723580	-10.947301	609.724272	-172.482377	-42.796400	59.174124	-162.912577	-112.219187	-55.108445	17.303261	-152.111164	-611.929832	181.577435	-211.358075	-77.180329	116.282095	83.488753	-26.254488	128.490023	-69.085253	4.854304	-128.278573	44.328867	-6.470515	-28.782209	14.618174	-31.359379	27.331179	-25.948771	8.941634	-34.840913	-21.933848	17.941556	-0.866531	-19.428832	-5.321193	6.319611	-11.398376	41.907093	-8.296132	0

1## Plotting principal components 
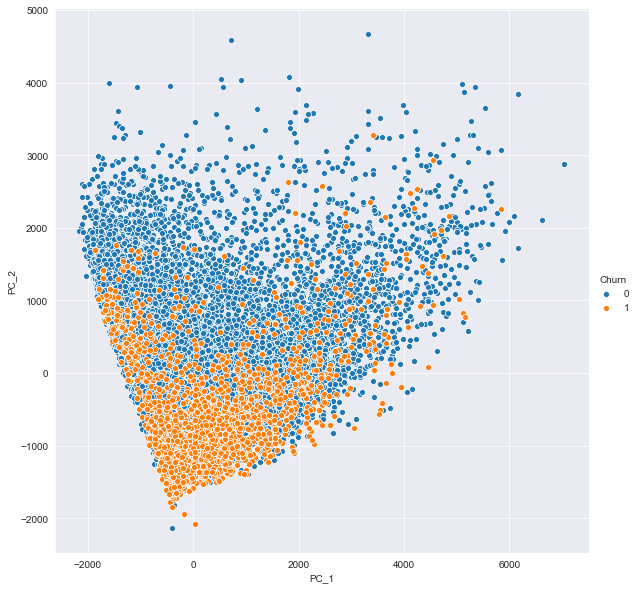
2sns.pairplot(data=data_train_pca, x_vars=["PC_1"], y_vars=["PC_2"], hue = "Churn", size=8);

Model 2 : PCA + Logistic Regression Model

1# X,y Split
2y_train_pca = data_train_pca.pop('Churn')
3X_train_pca = data_train_pca
4
5# Transforming test set with pca ( 45 components)
6X_test_pca = pca_final.transform(X_test)
7
8# Logistic Regression
9lr_pca = LogisticRegression(random_state=100, class_weight='balanced')
10lr_pca.fit(X_train_pca,y_train_pca )

1LogisticRegression(class_weight='balanced', random_state=100)

1# y_train predictions
2y_train_pred_lr_pca = lr_pca.predict(X_train_pca)
3y_train_pred_lr_pca[:5]

1array([1, 0, 0, 0, 0])

1# Test Prediction
2X_test_pca = pca_final.transform(X_test)
3y_test_pred_lr_pca = lr_pca.predict(X_test_pca)
4y_test_pred_lr_pca[:5]

1array([1, 1, 1, 1, 1])

Baseline Performance

1train_matrix = confusion_matrix(y_train, y_train_pred_lr_pca)
2test_matrix = confusion_matrix(y_test, y_test_pred_lr_pca)
3
4print('Train Performance :\n')
5model_metrics(train_matrix)
6
7print('\nTest Performance :\n')
8model_metrics(test_matrix)

1Train Performance :
2
3Accuracy : 0.645
4Sensitivity / True Positive Rate / Recall : 0.905
5Specificity / True Negative Rate :  0.62
6Precision / Positive Predictive Value : 0.184
7F1-score : 0.306
8
9Test Performance :
10
11Accuracy : 0.086
12Sensitivity / True Positive Rate / Recall : 1.0
13Specificity / True Negative Rate :  0.0
14Precision / Positive Predictive Value : 0.086
15F1-score : 0.158

Hyperparameter Tuning

1# Creating a Logistic regression model using pca transformed train set
2from sklearn.pipeline import Pipeline
3lr_pca = LogisticRegression(random_state=100, class_weight='balanced')

1from sklearn.model_selection import RandomizedSearchCV, GridSearchCV , StratifiedKFold
2params = {
3    'penalty' : ['l1','l2','none'], 
4    'C' : [0,1,2,3,4,5,10,50]
5}
6folds = StratifiedKFold(n_splits=4, shuffle=True, random_state=100)
7
8search = GridSearchCV(cv=folds, estimator = lr_pca, param_grid=params,scoring='roc_auc', verbose=True, n_jobs=-1)
9search.fit(X_train_pca, y_train_pca)

1Fitting 4 folds for each of 24 candidates, totalling 96 fits
2
3
4[Parallel(n_jobs=-1)]: Using backend LokyBackend with 4 concurrent workers.
5[Parallel(n_jobs=-1)]: Done  42 tasks      | elapsed:    4.0s
6[Parallel(n_jobs=-1)]: Done  96 out of  96 | elapsed:    6.9s finished
7
8
9
10
11
12GridSearchCV(cv=StratifiedKFold(n_splits=4, random_state=100, shuffle=True),
13             estimator=LogisticRegression(class_weight='balanced',
14                                          random_state=100),
15             n_jobs=-1,
16             param_grid={'C': [0, 1, 2, 3, 4, 5, 10, 50],
17                         'penalty': ['l1', 'l2', 'none']},
18             scoring='roc_auc', verbose=True)

1# Optimum Hyperparameters
2print('Best ROC-AUC score :', search.best_score_)
3print('Best Parameters :', search.best_params_)

1Best ROC-AUC score : 0.8763924253372933
2Best Parameters : {'C': 0, 'penalty': 'none'}

1# Modelling using the best LR-PCA estimator 
2lr_pca_best = search.best_estimator_
3lr_pca_best_fit = lr_pca_best.fit(X_train_pca, y_train_pca)
4
5# Prediction on Train set
6y_train_pred_lr_pca_best = lr_pca_best_fit.predict(X_train_pca)
7y_train_pred_lr_pca_best[:5]

1array([1, 1, 0, 0, 0])

1# Prediction on test set
2y_test_pred_lr_pca_best = lr_pca_best_fit.predict(X_test_pca)
3y_test_pred_lr_pca_best[:5]

1array([1, 1, 1, 1, 1])

1## Model Performance after Hyper Parameter Tuning
2
3train_matrix = confusion_matrix(y_train, y_train_pred_lr_pca_best)
4test_matrix = confusion_matrix(y_test, y_test_pred_lr_pca_best)
5
6print('Train Performance :\n')
7model_metrics(train_matrix)
8
9print('\nTest Performance :\n')
10model_metrics(test_matrix)

1Train Performance :
2
3Accuracy : 0.627
4Sensitivity / True Positive Rate / Recall : 0.918
5Specificity / True Negative Rate :  0.599
6Precision / Positive Predictive Value : 0.179
7F1-score : 0.3
8
9Test Performance :
10
11Accuracy : 0.086
12Sensitivity / True Positive Rate / Recall : 1.0
13Specificity / True Negative Rate :  0.0
14Precision / Positive Predictive Value : 0.086
15F1-score : 0.158

Model 3 : PCA + Random Forest

1from sklearn.ensemble import RandomForestClassifier
2
3# creating a random forest classifier using pca output
4
5pca_rf = RandomForestClassifier(random_state=42, class_weight= {0 : class_1/(class_0 + class_1) , 1 : class_0/(class_0 + class_1) } , oob_score=True, n_jobs=-1,verbose=1)
6pca_rf

1RandomForestClassifier(class_weight={0: 0.08640165272733331,
2                                     1: 0.9135983472726666},
3                       n_jobs=-1, oob_score=True, random_state=42, verbose=1)

1# Hyper parameter Tuning
2params = {
3    'n_estimators'  : [30,40,50,100],
4    'max_depth' : [3,4,5,6,7],
5    'min_samples_leaf' : [15,20,25,30]
6}
7folds = StratifiedKFold(n_splits=4, shuffle=True, random_state=42)
8pca_rf_model_search = GridSearchCV(estimator=pca_rf, param_grid=params, 
9                                   cv=folds, scoring='roc_auc', verbose=True, n_jobs=-1 )
10
11pca_rf_model_search.fit(X_train_pca, y_train)

1Fitting 4 folds for each of 80 candidates, totalling 320 fits
2
3
4[Parallel(n_jobs=-1)]: Using backend LokyBackend with 4 concurrent workers.
5[Parallel(n_jobs=-1)]: Done  42 tasks      | elapsed:   23.2s
6[Parallel(n_jobs=-1)]: Done 192 tasks      | elapsed:  2.7min
7[Parallel(n_jobs=-1)]: Done 320 out of 320 | elapsed:  5.5min finished
8[Parallel(n_jobs=-1)]: Using backend ThreadingBackend with 4 concurrent workers.
9[Parallel(n_jobs=-1)]: Done  42 tasks      | elapsed:    1.2s
10[Parallel(n_jobs=-1)]: Done 100 out of 100 | elapsed:    2.6s finished
11
12
13
14
15
16GridSearchCV(cv=StratifiedKFold(n_splits=4, random_state=42, shuffle=True),
17             estimator=RandomForestClassifier(class_weight={0: 0.08640165272733331,
18                                                            1: 0.9135983472726666},
19                                              n_jobs=-1, oob_score=True,
20                                              random_state=42, verbose=1),
21             n_jobs=-1,
22             param_grid={'max_depth': [3, 4, 5, 6, 7],
23                         'min_samples_leaf': [15, 20, 25, 30],
24                         'n_estimators': [30, 40, 50, 100]},
25             scoring='roc_auc', verbose=True)

1# Optimum Hyperparameters
2print('Best ROC-AUC score :', pca_rf_model_search.best_score_)
3print('Best Parameters :', pca_rf_model_search.best_params_)

1Best ROC-AUC score : 0.8861621751601011
2Best Parameters : {'max_depth': 7, 'min_samples_leaf': 20, 'n_estimators': 100}

1# Modelling using the best PCA-RandomForest Estimator 
2pca_rf_best = pca_rf_model_search.best_estimator_
3pca_rf_best_fit = pca_rf_best.fit(X_train_pca, y_train)
4
5# Prediction on Train set
6y_train_pred_pca_rf_best = pca_rf_best_fit.predict(X_train_pca)
7y_train_pred_pca_rf_best[:5]

1[Parallel(n_jobs=-1)]: Using backend ThreadingBackend with 4 concurrent workers.
2[Parallel(n_jobs=-1)]: Done  42 tasks      | elapsed:    1.1s
3[Parallel(n_jobs=-1)]: Done 100 out of 100 | elapsed:    2.7s finished
4[Parallel(n_jobs=4)]: Using backend ThreadingBackend with 4 concurrent workers.
5[Parallel(n_jobs=4)]: Done  42 tasks      | elapsed:    0.0s
6[Parallel(n_jobs=4)]: Done 100 out of 100 | elapsed:    0.1s finished
7
8
9
10
11
12array([0, 0, 0, 0, 0])

1# Prediction on test set
2y_test_pred_pca_rf_best = pca_rf_best_fit.predict(X_test_pca)
3y_test_pred_pca_rf_best[:5]

1[Parallel(n_jobs=4)]: Using backend ThreadingBackend with 4 concurrent workers.
2[Parallel(n_jobs=4)]: Done  42 tasks      | elapsed:    0.1s
3[Parallel(n_jobs=4)]: Done 100 out of 100 | elapsed:    0.1s finished
4
5
6
7
8
9array([0, 0, 0, 0, 0])

1## PCA - RandomForest Model Performance - Hyper Parameter Tuned
2
3train_matrix = confusion_matrix(y_train, y_train_pred_pca_rf_best)
4test_matrix = confusion_matrix(y_test, y_test_pred_pca_rf_best)
5
6print('Train Performance :\n')
7model_metrics(train_matrix)
8
9print('\nTest Performance :\n')
10model_metrics(test_matrix)

1Train Performance :
2
3Accuracy : 0.882
4Sensitivity / True Positive Rate / Recall : 0.816
5Specificity / True Negative Rate :  0.888
6Precision / Positive Predictive Value : 0.408
7F1-score : 0.544
8
9Test Performance :
10
11Accuracy : 0.914
12Sensitivity / True Positive Rate / Recall : 0.0
13Specificity / True Negative Rate :  1.0
14Precision / Positive Predictive Value : nan
15F1-score : nan

1## out of bag error 
2pca_rf_best_fit.oob_score_

10.8625220164707003

Model 4 : PCA + XGBoost

1import xgboost as xgb
2pca_xgb = xgb.XGBClassifier(random_state=42, scale_pos_weight= class_0/class_1 ,
3                                    tree_method='hist', 
4                                   objective='binary:logistic',
5                                  
6                                  
7                                  )  # scale_pos_weight takes care of class imbalance
8pca_xgb.fit(X_train_pca, y_train)

1XGBClassifier(base_score=0.5, booster='gbtree', colsample_bylevel=1,
2              colsample_bynode=1, colsample_bytree=1, gamma=0, gpu_id=-1,
3              importance_type='gain', interaction_constraints='',
4              learning_rate=0.300000012, max_delta_step=0, max_depth=6,
5              min_child_weight=1, missing=nan, monotone_constraints='()',
6              n_estimators=100, n_jobs=0, num_parallel_tree=1, random_state=42,
7              reg_alpha=0, reg_lambda=1, scale_pos_weight=10.573852680293097,
8              subsample=1, tree_method='hist', validate_parameters=1,
9              verbosity=None)

1print('Baseline Train AUC Score')
2roc_auc_score(y_train, pca_xgb.predict_proba(X_train_pca)[:, 1])

1Baseline Train AUC Score
2
3
4
5
6
70.9999996277241286

1print('Baseline Test AUC Score')
2roc_auc_score(y_test, pca_xgb.predict_proba(X_test_pca)[:, 1])

1Baseline Test AUC Score
2
3
4
5
6
70.46093390352284136

1## Hyper parameter Tuning
2parameters = {
3              'learning_rate': [0.1, 0.2, 0.3],
4              'gamma' : [10,20,50],
5              'max_depth': [2,3,4],
6              'min_child_weight': [25,50],
7              'n_estimators': [150,200,500]}
8pca_xgb_search = GridSearchCV(estimator=pca_xgb , param_grid=parameters,scoring='roc_auc', cv=folds, n_jobs=-1, verbose=1)
9pca_xgb_search.fit(X_train_pca, y_train)

1Fitting 4 folds for each of 162 candidates, totalling 648 fits
2
3
4[Parallel(n_jobs=-1)]: Using backend LokyBackend with 4 concurrent workers.
5[Parallel(n_jobs=-1)]: Done  42 tasks      | elapsed:   28.3s
6[Parallel(n_jobs=-1)]: Done 192 tasks      | elapsed:  2.1min
7[Parallel(n_jobs=-1)]: Done 442 tasks      | elapsed:  4.8min
8[Parallel(n_jobs=-1)]: Done 648 out of 648 | elapsed:  8.0min finished
9
10
11
12
13
14GridSearchCV(cv=StratifiedKFold(n_splits=4, random_state=42, shuffle=True),
15             estimator=XGBClassifier(base_score=0.5, booster='gbtree',
16                                     colsample_bylevel=1, colsample_bynode=1,
17                                     colsample_bytree=1, gamma=0, gpu_id=-1,
18                                     importance_type='gain',
19                                     interaction_constraints='',
20                                     learning_rate=0.300000012,
21                                     max_delta_step=0, max_depth=6,
22                                     min_child_weight=1, missing=nan,
23                                     monotone_...
24                                     n_estimators=100, n_jobs=0,
25                                     num_parallel_tree=1, random_state=42,
26                                     reg_alpha=0, reg_lambda=1,
27                                     scale_pos_weight=10.573852680293097,
28                                     subsample=1, tree_method='hist',
29                                     validate_parameters=1, verbosity=None),
30             n_jobs=-1,
31             param_grid={'gamma': [10, 20, 50],
32                         'learning_rate': [0.1, 0.2, 0.3],
33                         'max_depth': [2, 3, 4], 'min_child_weight': [25, 50],
34                         'n_estimators': [150, 200, 500]},
35             scoring='roc_auc', verbose=1)

1# Optimum Hyperparameters
2print('Best ROC-AUC score :', pca_xgb_search.best_score_)
3print('Best Parameters :', pca_xgb_search.best_params_)

1Best ROC-AUC score : 0.8955777259491308
2Best Parameters : {'gamma': 10, 'learning_rate': 0.1, 'max_depth': 2, 'min_child_weight': 50, 'n_estimators': 500}

1# Modelling using the best PCA-XGBoost Estimator 
2pca_xgb_best = pca_xgb_search.best_estimator_
3pca_xgb_best_fit = pca_xgb_best.fit(X_train_pca, y_train)
4
5# Prediction on Train set
6y_train_pred_pca_xgb_best = pca_xgb_best_fit.predict(X_train_pca)
7y_train_pred_pca_xgb_best[:5]

1array([0, 0, 0, 0, 0])

1X_train_pca.head()

	PC_1	PC_2	PC_3	PC_4	PC_5	PC_6	PC_7	PC_8	PC_9	PC_10	PC_11	PC_12	PC_13	PC_14	PC_15	PC_16	PC_17	PC_18	PC_19	PC_20	PC_21	PC_22	PC_23	PC_24	PC_25	PC_26	PC_27	PC_28	PC_29	PC_30	PC_31	PC_32	PC_33	PC_34	PC_35	PC_36	PC_37	PC_38	PC_39	PC_40	PC_41	PC_42	PC_43	PC_44	PC_45
mobile_number
7000166926	-907.572208	-342.923676	13.094442	58.813506	-95.616159	-1050.535219	254.648987	-31.445039	305.140339	-216.814250	95.825021	231.408291	-111.002572	-2.007256	444.977249	31.541681	573.831941	-278.539708	30.768637	-36.915195	-0.293915	-83.574447	-13.960479	-60.930941	-53.208613	56.049658	-17.776675	-12.624526	14.149393	-30.559156	26.064776	-1.080160	-19.814893	-3.293546	-2.717923	7.470255	22.686838	28.696686	-14.312037	4.959030	-8.652543	2.473147	17.080399	-21.824778	-8.062901
7001343085	573.898045	-902.385767	-424.839214	-331.153508	-148.987005	-36.955710	-134.445130	265.325388	-92.070929	-164.203586	25.105150	-36.980621	164.785936	-222.908959	-12.573878	-50.569424	-44.767869	-62.984835	-18.100729	-86.239469	-115.399141	-45.776518	16.345395	-21.497140	-10.541281	-71.754047	29.230830	-20.880178	-0.690183	3.220864	-21.223298	65.500636	-39.719437	50.424623	10.586150	43.055219	0.209259	-66.107880	13.583016	25.823444	52.037618	-3.272773	8.493995	19.449057	-38.779466
7001863283	-1538.198366	514.032564	846.865497	57.032319	-1126.228705	-84.209511	-44.422495	-88.158881	-58.411887	50.518811	3.052703	-229.100202	-109.215465	-3.253782	7.045279	-85.645393	54.536446	-52.292779	20.978943	-90.806167	96.348659	24.280381	-52.425262	42.430049	-40.627473	-12.715890	-4.331719	-4.092290	50.339358	-0.777645	-35.146663	-121.580965	98.868473	-34.068010	-8.941074	22.920757	1.669933	52.644942	-8.542762	9.087643	-18.403853	3.672076	26.073078	27.246371	19.603368
7002275981	486.830772	-224.929803	1130.460535	-496.189015	6.009139	81.106845	-148.667431	170.280911	-7.375197	-99.556793	-159.659135	-14.186219	-98.682096	213.233743	-34.920639	-17.212430	29.644778	4.941994	2.799763	-49.580528	-88.567855	16.809461	-9.471018	4.383889	29.532189	38.211558	32.465761	-5.316497	-60.149577	12.593305	20.988200	80.709846	-50.975160	-3.712583	65.002407	-57.837280	-8.312631	-5.931175	-5.053131	-5.667538	-12.102225	-14.690148	-32.215573	12.517731	-20.158820
7001086221	-1420.949314	794.071749	99.221352	155.118564	145.349456	784.723580	-10.947301	609.724272	-172.482377	-42.796400	59.174124	-162.912577	-112.219187	-55.108445	17.303261	-152.111164	-611.929832	181.577435	-211.358075	-77.180329	116.282095	83.488753	-26.254488	128.490023	-69.085253	4.854304	-128.278573	44.328867	-6.470515	-28.782209	14.618174	-31.359379	27.331179	-25.948771	8.941634	-34.840913	-21.933848	17.941556	-0.866531	-19.428832	-5.321193	6.319611	-11.398376	41.907093	-8.296132

1# Prediction on test set
2X_test_pca = pca_final.transform(X_test)
3X_test_pca = pd.DataFrame(X_test_pca, index=X_test.index, columns = X_train_pca.columns)
4y_test_pred_pca_xgb_best = pca_xgb_best_fit.predict(X_test_pca)
5y_test_pred_pca_xgb_best[:5]

1array([1, 1, 1, 1, 1])

1## PCA - XGBOOST [Hyper parameter tuned] Model Performance
2
3train_matrix = confusion_matrix(y_train, y_train_pred_pca_xgb_best)
4test_matrix = confusion_matrix(y_test, y_test_pred_pca_xgb_best)
5
6print('Train Performance :\n')
7model_metrics(train_matrix)
8
9print('\nTest Performance :\n')
10model_metrics(test_matrix)

1Train Performance :
2
3Accuracy : 0.873
4Sensitivity / True Positive Rate / Recall : 0.887
5Specificity / True Negative Rate :  0.872
6Precision / Positive Predictive Value : 0.396
7F1-score : 0.548
8
9Test Performance :
10
11Accuracy : 0.086
12Sensitivity / True Positive Rate / Recall : 1.0
13Specificity / True Negative Rate :  0.0
14Precision / Positive Predictive Value : 0.086
15F1-score : 0.158

1## PCA - XGBOOST [Hyper parameter tuned] Model Performance
2print('Train AUC Score')
3print(roc_auc_score(y_train, pca_xgb_best.predict_proba(X_train_pca)[:, 1]))
4print('Test AUC Score')
5print(roc_auc_score(y_test, pca_xgb_best.predict_proba(X_test_pca)[:, 1]))

1Train AUC Score
20.9442462043611259
3Test AUC Score
40.6353301334697982

Recommendations

1print('Most Important Predictors of churn , in the order of importance are : ')
2lr_results.sort_values(by=coef_column, key=lambda x: abs(x), ascending=False)['coef']

1Most Important Predictors of churn , in the order of importance are : 
2
3
4
5
6
7loc_ic_t2f_mou_8   -1.2736
8total_rech_num_8   -1.2033
9total_rech_num_6    0.6053
10monthly_3g_8_0      0.3994
11monthly_2g_8_0      0.3666
12std_ic_t2f_mou_8   -0.3363
13std_og_t2f_mou_8   -0.2474
14const              -0.2336
15monthly_3g_7_0     -0.2099
16std_ic_t2f_mou_7    0.1532
17sachet_2g_6_0      -0.1108
18sachet_2g_7_0      -0.0987
19sachet_2g_8_0       0.0488
20sachet_3g_6_0      -0.0399
21Name: coef, dtype: float64

From the above, the following are the strongest indicators of churn

Customers who churn show lower average monthly local incoming calls from fixed line in the action period by 1.27 standard deviations , compared to users who don’t churn , when all other factors are held constant. This is the strongest indicator of churn.
Customers who churn show lower number of recharges done in action period by 1.20 standard deviations, when all other factors are held constant. This is the second strongest indicator of churn.
Further customers who churn have done 0.6 standard deviations higher recharge than non-churn customers. This factor when coupled with above factors is a good indicator of churn.
Customers who churn are more likely to be users of ‘monthly 2g package-0 / monthly 3g package-0’ in action period (approximately 0.3 std deviations higher than other packages), when all other factors are held constant.

Based on the above indicators the recommendations to the telecom company are :

Concentrate on users with 1.27 std devations lower than average incoming calls from fixed line. They are most likely to churn.
Concentrate on users who recharge less number of times ( less than 1.2 std deviations compared to avg) in the 8th month. They are second most likely to churn.
Models with high sensitivity are the best for predicting churn. Use the PCA + Logistic Regression model to predict churn. It has an ROC score of 0.87, test sensitivity of 100%

Telecom Churn Case Study - Part 2

Telecom Churn Case Study - Part 2

Train-Test Split

Class Imbalance

Using SMOTE

Standardizing Columns

Modelling

Model 1 : Interpretable Model : Logistic Regression

Baseline Logistic Regression Model

Baseline Performance at Optimum Cutoff

Feature Selection using RFE

Logistic Regression with RFE Selected Columns

Model I

Logistic Regression with Manual Feature Elimination

Model II

Model III

Final Logistic Regression Model with RFE and Manual Elimination

Performance

Model 1 : Logistic Regression (Interpretable Model Summary)

PCA

Scree Plot

Model 2 : PCA + Logistic Regression Model

Hyperparameter Tuning

Model 3 : PCA + Random Forest

Model 4 : PCA + XGBoost

Recommendations

More articles from Yugen

Lead Scoring for X Education

Countries in need of Aid

	0.0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
0	1	1	0	0	0	0	0	0	0	0
1	1	1	1	1	0	0	0	0	0	0
2	1	1	1	1	0	0	0	0	0	0
3	1	0	0	0	0	0	0	0	0	0
4	1	0	0	0	0	0	0	0	0	0

	0.0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
0	1	1	0	0	0	0	0	0	0	0
1	1	1	1	1	0	0	0	0	0	0
2	1	1	1	1	0	0	0	0	0	0
3	1	0	0	0	0	0	0	0	0	0
4	1	0	0	0	0	0	0	0	0	0

	0.0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
0	1	1	0	0	0	0	0	0	0	0
1	1	1	1	1	0	0	0	0	0	0
2	1	1	1	1	0	0	0	0	0	0
3	1	0	0	0	0	0	0	0	0	0
4	1	0	0	0	0	0	0	0	0	0